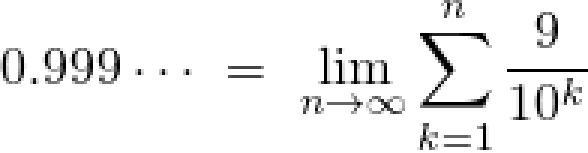- 다양한 주제에 대해 자유롭게 글을 작성하는 게시판입니다.
| Date | 18/09/09 15:53:28 |
| Name | 파랑새의나침반 |
| File #1 | LaTeX.jpg (16.0 KB), Download : 35 |
| Subject | 0.999...는 어디서 왔는가? 0.999...는 무엇인가? 0.999...는 어디로 가는가? |
|
Ein Gespenst ist noch wie eine Stelle, dran dein Blick mit einem Klange stößt; aber da, an diesem schwarzen Felle wird dein stärkstes Schauen aufgelöst: 이것에서 사람들은 유령을 보았습니다. 유령에 홀린 것만 같은 사람들입니다. 수학에 유령이 존재합니다. 최대한 수학을 이야기하고 싶었던 이 글은 무엇인가 문제에 빠져 그 뜻을 잃어버리고 또다른 비자명적인 주제로 나아가야 했다. 글은 일반적인 수학 공식과 정리와 이론으로 끝날 수 없었습니다. 유령은 그렇게 달랐습니다. 저는 유령이 존재함을 확신하기 때문입니다. 유령은 말한다. 나는 선지자가 아니다. 나는 벽이 있는 곳에 창문을 달아주기만 할 뿐이다. 의미와 관련없이 "담론" 이라는 언어를 붙이겠습니다. 0.999...에 대한 담론을 정리하려고 합니다. 소모적이고 지속적인 이 긴 시간동안 담았던 것이 무엇이었을까요. 사람들은 왜 이 유령에 홀려 있던 것일까요. 먼저 Promise를 하나 두겠습니다. Promise 1. 0.999...가 1인지 1이 아닌지에 있어 물질적이거나, 실체적인 것이 답의 근거가 될 수 없다. 이 Promise를 결정한 이유는 0.999...에 대한 논쟁에서 가장 많이 나오는, 다음과 같은 담론을 막기 위해서입니다. Question 1. "0.999...가 자연상태에 있는 거냐? 저런 수가 정말로 세상에 존재할 수 있는 것이냐?" "0.999...에 9가 끝없이 이어졌다는 것이 어떤 효용성을 가진다는 건데?" "무한대와 인간의 삶의 연관성은 없다. 무한대의 존재론과 가치를 설명할 수 없지 않느냐?" 무색해졌고, 전에 너무나 많이 진행되었습니다. 이 담론을 주제로 정하는 것은 피로도를 높일 뿐입니다. Promise라고 두고 이것을 제외하는 것이 옳다고 결정하였습니다. Answer 2. "0.999... = 1 에 대해, 0.999...를 S라고 둔다. S = 0.999... 10S = 9.999... 10S - S = 9 9S = 9 S = 1" 의미와 관련없이 "intuition" 이라는 언어를 붙이겠습니다. intuition이란 단어를 생각할 수 있습니다. 혼란 속 아이를 위한 intuition이라고 생각합니다. 유령에 홀린, 0.999... = 1 을 믿지 않는 사람들은, 이것이 쓸모가 없어집니다. "1/3 = 0.333..." 로 진행되는 증명도 같이 생각할 수 있습니다. 같은 형태의 함정을 가진 증명들입니다. 0.999... = 1의 증명에 직접 접근하려 드는 것이 아니라 이 문제를 좀 더 덜 모순되어 보이는 다른 문제로 바꾼 것입니다. 이런 접근에서 다른 문제가 나옵니다. 문제를 다른 문제로 옮기는 과정이 참이었는지를 보여야 하고, 과연 그 다른 문제가 정말 참일 수 있는지도 보여야만 할 것입니다. 1/3 이야기가 그렇게 각광받지 않는 이유는 무엇일까요. 나쁘게 말하자면, 1/3은 아이를 함정에 빠뜨리기에도 너무 단순한 것이라서겠죠. 이것을 대답이라고 할 수 없습니다. 아래에는 사람들을 위한 Question이 존재할 것입니다. Answer 2에 대한 - Question 2 - 1. 극한은 성질 X을 가지고 있지 않음을 증명하겠다. 성질 X가 있다고 가정한다. 0.999...를 S라고 두자. S = 0.999... 10S = 9.999... 10S - S = 9 9S = 9 S = 1 0.999... = 1 이다. 따라서 극한은 성질 X를 가지고 있지 않다. Question 2 - 2. 우리가 저학년때 배운(받아들인) 정리 중에서 "수렴하는 수열 A_n, B_n이 있고 모든 자연수 n에 대해 A_n > B_n 이면, lim A_n 은 lim B_n 보다 크'거나 같다' " 가 있듯이, 수열의 극한 등의 극한을 다루는 수학적 구조들은 기존에 쓰던 "우리가 아는 것" 과 다름이 틀림없다. 우리가 명확하다고 본 다른 수들과 같은 규칙을 가지지 않을 거라는 것이다. 그런데 이러한 불명확한 주제를 어찌 그리 자유자재로 쓸 수 있다는 것인가? 명확성이 없는 현 상황에서, 이것은 증명이 아니라 조작이라고 봐야 한다. 극한이 과연 어떤 기능을 가지는지, 과연 사칙연산을 포함한 기존의 수학에서 어떤 대응성을 가질지 제대로 된 접근이 나와있지 않기 때문이다. 다음을 통해서 더 간단히 설명해보겠다. 1/3 = 0.333... 이므로 3/3 = 0.999... = 1 이라는 증명은, 0.999... 가 1이라는 것을 증명해주는 것이 아니라 오히려 1/3이 0.333... 이 아님을 증명해준다고 할 수 있지 않는가? 이제 S에 대한 사례로 넘어가겠다. 이것이 "9.999... - 0.999... = 9" 가 아님을 증명하는 것이 아니라고 자신할 수 있는가? 이것이 "S가 0.999... 일 때 10S는 9.999... 이다" 가 아님을 증명하는 것이 아니라고 자신할 수 있는가? 이것이, 심지어는, "0.999... 를 S라고 둘 수 있다" 가 아님을 증명하는 것이 아니라고 자신할 수 있는가? Question 2 - 3. 9.9 - 0.99 = 8.91 9.99 - 0.999 = 8.991 9.999 - 0.9999 = 8.9991 ... 따라서 9S = 9가 아니라 8.999... 이다. 문제를 함축하는 것이 좋을 것 같습니다. Question 2는, 이야기가 상당한 합리성을 보일지라도 엄밀성은 갖추지 못할 수 있음을 호소합니다. 0.999...는 0.999... 그 존재 자체와, 그에 있는 극한을 이야기해야 함을 호소합니다. 이곳에서 저는 Thesis를 제시하겠습니다. Thesis 1. 0.999... 에 대하여, 다음은 인정된다. [사진] (Thesis는 theorem이 아닙니다. 이것은 유령을 더 쉽게 보기 위한 편의에 지나지 않습니다.) Answer 3 : [ 단조증가하는 수열이 유계하면 수렴한다는 것 따위의 증명은 넘기겠다. 너도 자명하다고 받아들일 테니까. ] e>0이 주어졌다고 보자. 1 / 10^N < e 를 만족하는 자연수 N을 둘 수 있다. 1 - {sigma (1 to n) 9 / 10^n} = 1 / 10^n 이다. N 이상의 자연수 n에 대해 dist(x_n - x) = 1 / 10^n 1 / 10^n < 1 / 10^N < e. 임의의 e>0에 대하여 자연수 N이 존재하여 N 이상인 자연수 n에 대해 dist(x_n - x)이 e>0보다 작음을 보였다. 따라서 0.999... = 1이다. 이것이 바로 해석학을 도입한 대답, 현재까지의 0.999... 담론에서 가장 이상적이라고 판단되는 그 논법을 사용한 대답입니다. 왜 이 논법은 Answer라고 받아들여질까요. 이 Answer 자체가 극한을 다루지 않는다는 점에 있을 것입니다. 무한이 없습니다. 사람들이 주장했던 "아주 조그만 그 무언가" 도 없습니다. 문제에서도 있었던 ...마저 없습니다. 0.999...를 1로 인정하지 않는 사람들의 경우에도 1 - {sigma (1 to n) 9 / 10^n} = 1 / 10^n 은 그들이 생각하는 수학적 구조, "우리가 아는 것" 내에서 참인 식이기에 인정할 것입니다. 그렇게 더 이상 엄밀히 정해지지 않았던 다른 개념들을 쓸 이유가 없어졌다는 것이죠 ... 글쎄요. 이 Answer 자체가 극한이란 점에 있을 것입니다. 증명을 위해 극한 그 자체에 논법을 도입해야 했습니다. 모든 극한을 어떻게 제시해야 하는지를 전부 설명할 수 있으며, 이를 쓰지 못하는 모든 것을 극한이 아니라고 할 수 있어야 했습니다. 그렇기 때문에 이것을 Answer라고 받아들일 수 있던 것입니다. Thesis 2. 0.999...가 1임을 보이는 증명들은 평범한 수학 정리의 증명과는 다른 점을 보인다. 이것들은 극한을 어떻게 정의했는지 논법을 제시한 것에 가깝다. 0.999... = 1의 "증명"들은, 증명이라기보단 극한을 어떻게 생각했는지 알린 것과 다름없다. 현재 제가 아는 논법 중에서, 가장 마음에 든 증명은 다음과 같았습니다. "실수 체계에서 infinitesimal은 0밖에 없다." Question 3. 그 어떤 자연수 N을 두더라도 1 / 10^N < e 가 성립하지 않는 e>0가 있을 수 있지 않은가? Answer 4. 그 질문을 할 것이라고 전부터 예측하고 있었다. 1 / 10^N < e 을 고치면 - log_10 e < N 이라는 식으로 바꿀 수 있다. 따라서 이 문제는 "e>0에 대한 어떤 큰 수 - log_10 e을 제시했을 때, 이보다 더 큰 자연수 N이 존재하지 않을 수 있다" 와 동치가 될 것이다. 이것은 실수 체계의 성질 중 하나인 Archimedean property 에 의해 불가능하다. 따라서, 그러한 e>0는 존재하지 않는다. Question 4. 왜 실수 체계를 써야만 하는가? The Pharcyde - Runnin' 유령은 이렇게 말한다... 광기는 잘못된 답에 대한 잘못된 처벌이다. 이를 실로 해결하는 방법은 문제의 실상을 비추는 것에 있기 때문이다. "왜 실수 체계를 써야만 하는가?" "해석학이 실수 내에서 이루어지고, 실수가 해석학의 근간이 된다면, 실수는 무엇이란 말인가?" "실수가 아직 진리라고 밝혀지지 않았으므로, 나는 0.999...가 1이라 하지 않겠다." 달라진 것은, 사람입니다. 사람들은 그와 이야기를 하지 않습니다. 해석학도 그를 이해하는 데엔 쓸모가 없습니다. 그를 그저 유령에 홀린, 광기에 빠진 사람으로 보지 않고 그에게서 더 깊은 수평을 보아 뿌리가 보이지 않는 무언가를 보게 하기에는 님들을 움직일 수 있을 글을 쓸 능력이 저에게 없습니다. 저는 이곳에서 Promise 2를 결정하였습니다. Promise 2. 더 나아가려는 과정은, 실재해야 한다. Question에서 제시되었던 많은 극한의 성질을 설명할 수 있었고 그러한 해석학은 실수 체계 위에서 가능케 하였습니다. 하지만 유령은 실수 체계에 있지 않아 보입니다. 해석학은 Answer를 제시할 수 있습니다. 해석학은 왜 그 Answer인지를 제시할 수 있습니다. 해석학은 Answer를 제시했다는 것이 무엇을 뜻하는지 제시할 수 없습니다. [해석학은 무엇을 해석한 것인가요?] 아직, 아직은 0.999... = 1 은 진리라고 할 수 없습니다. "실수 체계는 진리를 다룬다" 라는 이야기가 있어야 하기 때문입니다. 이를 위해서는, 혼란스러워할 님들을 위한 intuition이 필요합니다. Thesis 3. 다음을 만족하는 H-real number가 존재한다. 0. hyperreal number와 "닮았다". 크게 보면, real number와도 "닮았다". 1. 수열의 극한과 함수의 극한을 설명할 수 있다. 2. 뉴턴과 라이프니츠의 원시적 미적분학 이론과의 대응성을 보인다. 3. Archimedean property를 부정하며, 무한히 많은 infinitesimal이 정의된다. 4. 이 H-real 체계 내에서는 0.999... = 1-e 이다. 1-e = 1, e = 0, H-real 체계 내에서 e가 0인 것이 필연적이지 않다. 따라서 0.999... = 1은 부정된다. "실수라는 존재가 진리와 동치이기 위한 이성적인 이유가 과연 무엇인가?" 이에 대한 Claim들을 4가지로 함축하고 각각을 이야기하고자 합니다. 이야기는 전부 뒤틀려 있습니다. Claim 1. 심미성 Archimedean property라는 것은 충분히 직관적이다. 또한, H-real number와 같이 무한소와 같은 개념이 있을 경우 미적인 깔끔함을 보여주지 않는다. 유클리드 공간의 기하학적인 심미성을 볼 때 완비성이 있는 실수 체계가 깔끔함과 직관성을 유발한다. 이러한 심미성이 바로 실수 체계를 쓰는 이유이다. Claim 1에 대한 비판. - 엄밀하게 보면, Archimedean property도 직관적이지 않다. Archimedean property는 우리가 다루는 평범한 수에서는 직관적이다. 하지만 언제나 이것이 직관적인가? 우주의 원자의 수보다 큰 수, 예를 들어서 구골과 같은 실수가 있다는 것을 직관할 수 있는가? 이에 더해서 그러한 실수보다 더 큰 실수가 항상 존재한다는 것을 생각할 수 있는가? 이에 더해서, "그 어떤 0보다 더 큰 수 e에 대해서도 충분히 그 자신을 계속 더한다면 2^2^구골플렉스 보다 더 커질 수 있다" 가 사실이라고 느껴지는가? 한번 여기서 묻겠다. "어떤 작은 수 e>0은, 그 자신을 계속 더해도 2^2^구골플렉스보다 커질 수 없다" 라는 명제는 꽤 직관적이지 않은가? - "깔끔함" 이 무엇인가? 실수 체계가 완비성과 유클리드 공간과의 대응성이 있어서 깔끔하다면, 원시적인 미적분학 이론과 대응성이 있고 미적분학을 깔끔하게 설명할 수 있는 H-real number는 깔끔하지 않다는 것인가? 애초에 깔끔함을 원한다면 완비성도 제외하고 오직 분수만으로도 모든 형태를 표현할 수 있는 유리수만을 인정하는 것이 옳지 않은가? 그리고 깔끔함은 규칙을 가지지 않을 것이다. 깔끔함을 어찌 그리 자유자재로 쓸 수 있다는 것인가? 깔끔함은 깔끔하지 않은 다른 문제들을 함의할 수 있다. 완비성이 깔끔하다고 생각하는가? 유클리드 공간의 깔끔함을 위해 완비성을 인정하는 것이 옳다고 보는가? 0.999...가 1인지 1이 아닌지를 다루는 지금 이 문제 그 자체가 그 "깔끔함" 을 깔끔하지 않다고 생각한 사람들 때문에 나온 것이다. - 심미적인 요소는 수학적인 요소를 결정해서는 안 된다. 과거, 고대 그리스의 학자들은 진실이라는 것과, 좋다는 것과, 아름다운 것이 모두 같은 방향을 바라보고 있다고 보았다. 진, 선, 미 가 결국에는 모두 동일한 것이라고 보았다. 하지만 시간이 지나면서 이 의견은 비판을 받게 되었다. 당신도 이 비판의 당위를 이해할 수 있을 것이다. 아름다워도 악한 사람이 있다는 것, 선한 거짓말이 있다는 것, 그리고 진실이 꼭 아름다운 것이 아니라는 것을 말이다. 이러한 비판을 이해할 수 있는 것처럼, 심미성이 수학을 결정해서는 안 된다. 수학의 몇몇 공식들, 정리들, 이론들이 아름다울 수 있음을 이해한다. 하지만 이것만이 수학인가. Claim 2. 역사성 Archimedean property의 경우, 유클리드의 원론에서 나올 만큼 그 개념이 오래되었다. 이는 고대에서부터 현대까지 참이라고 여기고 계속 써왔던 것이다. H-real number를 쓰게 된다면 Archimedean property 따위를 부정함으로서 기존까지 탐구해오던 수학자들의 성과를 회피하는 일이 될 것이고, 이는 바람직하지 않다. 이러한 역사성이 실수 체계를 쓰는 이유이다. Claim 2에 대한 비판. - 유클리드의 원론과 그를 받아들인 수학자들만이 수학의 역사인가? 선사 시대에도 기본적인 양의 정수의 덧셈과 뺄셈이 있었다는 고고학적 발견이 있다. 또한 역사성으로 보자면 그리스 로마 시대의 이러한 발전은 이집트와 바빌로니아의 기하학적 사료의 결과물이 아닌가. 여기에 원론과 관련이 없음에도 역사성을 가지는 수학이 있다. 인도의 베다 수학은 원론보다 전부터 발전이 있었고, 그 인도의 Kerala 학파라는 곳은 뉴턴과 라이프니쯔보다 앞선 1300년대에 현재의 무한 급수와 테일러 급수 등을 적시하였고, 중국에서도 수학의 발전이 있어 조충지는 원주율을 연구하여 전 세계적으로 900년동안, 유럽에서는 1100년동안 앞서지 못했던 근삿값을 두었다. 이들을 역사성을 가진다고 볼 것인가? 원론만이 특수해야 할 이유가 무엇인가? - 실수가 진실로 님이 주장하는 역사성을 지니는가? Archimedean property라고 하지만, 바로 그 아르키메데스야말로 infinitesimal라는 개념을 써서 원주율을 구하려던 사람이 아니었는가? 유클리드의 원론에서도 Archimedean property가 적시되었을 뿐 Completeness에 대한 개념은 빈약했다. infinitesimal이야말로 페르마가 그 당시의 수가 가지지 않는 성질을 고안한 뒤 뉴턴과 라이프니츠가 태어나 미적분학을 개발하면서 계속 쓰여왔던 것 아니었는가? 이러한 학문의 발전 뒤에야 다른 개념들을 실수에 종속하려는 시도가 있었던 것이다. 진정 실수가 엄밀하게 정의되었던 때는 데데킨트가 어느 정도의 무한 집합의 개념을 도입하고 데데킨트 절단의 개념을 쓴 1863년이다. 겨우 150년 정도밖에 지나지 않은 체계가 무슨 역사성이 있단 말인가. Claim 3. 약속성. 이미 0.999... 와 1이라는 숫자가 있을 때부터, 우리는 그저 실수 내에 있는 0.999... 라는 수, 1이라는 수로 대입할 뿐이다. 수학자들이 다른 수 체계 대신 실수 체계를 쓰겠다고 약속했기 때문이다. 1 + 1 을 10이라고 틀린 주장을 하는 사람에게 틀렸다고 하자, 나는 그저 2진법을 썼을 뿐이라며 맞다고 주장하는 사람이 있다 하자. 이 사람이 틀린 이유는 그저 수학자들이 10진법을 쓰자고 약속했기 때문이다. 만약에 당신이 H-real number를 쓰겠다면 그걸 쓰겠다고 먼저 명시를 하면 된다. 그저 수학자들은 실수 체계를 쓰자고 약속한 것일 뿐이다. 이러한 약속성이 실수 체계를 쓰는 이유이다. Claim 3에 대한 비판. - H-real number를 앞서 명시했으면 된다는 것으로 이야기는 끝날 수 없다. 이것은 실수 체계가 H-real number와 비교하여 앞서는 이유, 약속성을 가지는 이유를 설명하지 못한다. 실수의 존재성만큼 H-real number에 대해 명시로 존재성을 둘 수 있다면, 이들이 0.999...를 포함한 많은 형태에서 상호모순임을 회피하는 것이다. 애초에, 진리를 두어야 할 수학에서 왜 약속이란 장치가 필요하단 말인가? 약속에 어떤 진리가 있단 말인가? 당신들이 예로 든 것을 다시 생각해본다. 1+1을 10이라고 한 사람이 진리가 아닌 이유는, 약속이 2진법이 아니라 10진법이었기 때문이었다. 약속은 그것밖에 의미하지 않는다. 실수 체계 0.999...가 1이 아닌 진리만큼만 실수 체계가 진리적이었다. 진리는 어디에도 없고 남는 것은 공허함인가. 약속이 무엇이었는지만에 따라서 결정되는 것이 수학인가. - 이것이 약속성이라면, 수학은 말그대로 약속성을 꾸준히 부숴감으로서 발전해 나아갔다. 유리수를 계속 유지하려고 했던 피타고라스 학파에 대응하여 무리수가 생겨났고, 제곱해서 음수가 되는 수를 제대로 쓰지 않기로 약속한 시간을 오일러는 바꾸려고 했으며, 평행선 공준이라는 약속을 인정하지 않고 직선과 평행선의 말의 선천성을 벗어남으로서 비유클리드 기하학과 리만 기하학이 나왔다. 수많은 사람들이 약속을 두던 자연수에 대해서도 그리스만은 의문을 던졌다. 수학의 많은 자연수를 사용한 정리가 재귀적인 함수 정도로도 증명이 가능하다는 그의 내용은, 데데킨트에게 자연수의 공리적 접근과, 집합론의 일부를 보이게 된 계기가 되고 현대 수학의 첫걸음이 되었다. 실수 체계를 약속으로 두겠다는 것은 실수가 진리가 아니라는 신호탄이다. 약속을 지키려는 수학자들은 수학의 발전을 막는 것을 목적할 뿐이다. 유령은 이렇게 말했다. 선한 자들은 그 우둔함이 이루 말할 수 없이 영리하다. 선한 자들은 그들의 선을 만들어내는 자를 제물로 바칠 수밖에 없다. 선한 자들은 창조할 수 없다. 그들은 언제나 종말의 시작이다. 역사는, 수학자들의 약속은 앞에 가정이란 가능성을 양상으로 두고 있다. 코시와 바이어슈트라스가 실수를 만들어 내던 19세기 초반에도 볼차노가 있었고, 그리스만이 있었고, 갈루아가 있었다. 그리고 이곳에 가능성을 둔다. 수학이 무엇인지 볼 수 있었던 사람이 있었다. 수학에 Amour가 있음을, 자유가 있음을, 독립이 있음을 본 사람이 있었다. 그 사람이 나왔다면 어떻게 할 것인가? 그 사람은 이렇게 말했다. "고전이 된 명제 'Magnitudes are said to have a ratio to one another which can, when multiplied, exceed one another.' 는 오직 크기와 비율에 기초를 둔 문제에서만 명백한 명제가 되어 적용할 수 있을 것이다. 하지만, 이 '공리'는 무수히 많은 상황에서 그 기저가 없이 쓰이며, '실제'와 '수학'의 필연적인 구별이 무시되고 있다. 수학은 이 명제와 명확히 반대될 수 있다." 그는 H-real number를 생각했다. 수학자들은 H-real number를 따르고, 수학자들의 성과들 속에 H-real number가 자리잡게 되었다. H-real number는 수학자들의 약속이 되었다. 역사성을 생각한 당신은 실수 체계를 버릴 것인가? 약속성을 생각한 당신은 실수 체계를 버릴 것인가? Claim 4. 위상수학이라는 것이 있다. 위상수학에서 주로 다루는 구조들은 전에까지 다루던 유클리드 공간보다 훨씬 적은 조건밖에 두지 않은 뒤 어떤 정리가 어디까지 보존될 수 있는지에 대해 어렵게 증명하려고 든다. 위상수학을 공부하면 느낄 수 있는 것들이 있어. 몇몇 성질들이 없으면 당연하게 받아들여온 정리가 얼마나 까다롭게 될 수 있는지, 특수한 조건을 추가하지 않을 때 얼마나 다룰 내용이 없을 수 있는지, 유클리드가 얼마나 성질이 좋은 곳인지. 성질이 좋지 않으면 수학에서 이야기할 게 없어. 한 번 생각해보자. 하우스도르프도 되지 않는 곳에서 어떤 주목할 점이 있을 것 같아? 이야기를 이해해. hyperreal number는 기존 실수 체계에 무한대와 무한소를 넣었고 그에 대한 사칙연산도 큰 문제가 없다고 해도 괜찮다고 봤어. 하지만 알아줘야 할 게 있어. 실수 체계는 유리수에 데데킨트 절단을 쓴 것으로 정의하지만, 실수 체계가 유리수에 데데킨트 절단을 쓴 것뿐만이 아니야. 푸리에 해석이 얼마나 많은 곳에 쓰일 수 있는지. 아벨 정리를 아벨 정리로 만들기 위해 어떤 다른 정리를 인정했는지. 실수 체계를 두지 않았으면 리만 제타 함수가 이런 형태를 갖출 수 있었을지. 수많은 해석학의 정리들을 보존하는 데엔 실수 체계의 Completeness가 필요했어. 수학자가 hyperreal을 쓰지 않는 이유가 뭔지 알아? hyperreal은 성질이 좋지 않기 때문이다. 실수 체계와 비교할 때 도움을 주지 못하는 성질의 문제가 있다. 수학으로 이야기하기에 나쁜 것이다. ... hyperreal에 neighborhood로 topology 구성을 시도해보자. real에서는 (r-e , r+e) 인데 hyperreal에서는 그대로 쓸 수는 없겠지. 그러면, hyperreal에서도 쓰기 위해서는 r과 e 이 둘을 오직 real number라고 한정하겠다. 그리고 (r-e , r+e) 인 hyperreal을 전부 해당하지만, r-e와 r+e라는 두 실수에서는 infinitesimal하게도 가깝지 않아야 한다고 규정해 보자. 그 원소들의 모임을 집합이라고 두어서 neighborhood를 구성할 수 있을 거고, 이것으로 topology를 만들 수 있다. 위상수학에서 neighborhood는 굉장히 중요한 의미를 가진다. 이 topology가 hyperreal 위에서의 topology 중 굉장히 well-behaved할 topology라 짐작할 수 있을 거야. 하지만 이렇게 만든 topology는 실수 부분을 공유하는 두개의 다른 hyperreal을 제시했을 때 그 어떤 neighborhood를 제시하더라도 그 교집합을 공집합으로 만들 수 없어. 이 well-behaved하다는 topology마저도, 하우스도르프가 아니야. (하우스도르프가 되도록 조정한 topology에선 다른 중요한 부분이 부정되어 더 심각하게 not well-behaved해.) 이렇게 좋지 않은 성질 위에서는 어떤 문제를 일으키느냐. 다른 분야에서 쓰이는 정리들을 제대로 적용하기 어려울 지도 몰라. 증명 방법에 제한이 있어서 더 긴, 더 지저분한 증명으로 대체해야 할 거야. 어떤 성질은 그 어떤 방법으로도 다시는 쓰지 못할 거야. 존재합니다. 선택공리를 써야 하는지, 의존 선택 공리를 선택 공리 대신 써야 하는지 수학의 기저에는 무엇을 두고, 함수의 domain에 무엇을 두어야 하는지. 그리고 실수 체계와 hyperreal 중에서 무엇이 옳은 것인지. 이런 것을 다루기 위한 집합론, 수리논리학, 수학기초론 과 같은 것이 존재하지만, 이것이 수학의 이야기냐고 말한다면 전혀 아니라고 말하고 싶습니다. 오히려 가장 동떨어진 곳에 가깝습니다. 이런 수학을 문제라고 보고 바꾸려는 시도는 전에도 수없이 있어왔지만, 그 시도들은 그 시도대로 정말로 이상한 결과를 보여줬습니다. 지나치게 논리적인 측면만을 두려고만 하고. 그 접근으로부터 오히려 더 이상한 정리들이 나왔습니다. 기존에 멀쩡히 있어왔던 수학들을 떼네어서 포기하려 하고. 귀류법을, Law of excluded middle을 포기하려는 것을 수학자들은 이해하기 힘들어 합니다. 이들이 하는 이야기는 수학이라고 부르기 힘들 정도로 수학의 색조를 찾아볼 수 없습니다. 왜 수학에서 이 이야기를 하려고 합니까? [ ... 사실은, 글의 방향을 볼 때 착각을 일으킬지도 모를 문장이 있습니다. 지저분한 증명이 나옵니다. 까다로운 부분도 있습니다. 성질이 좋지 않기도 합니다. 하지만 hyperreal을 사용한다는 것이 이야기가 없다는 것이 아닙니다. hyperreal 안에서도 해석학이 있고 그것만의 정리가 있어서, 무엇보다도 수학의 다른 분야에 가까이 가는 데에는 전혀 문제가 될 것이 아무것도 없습니다. 중요한 것은 Hyperreal이 실수 체계와 비교하여 성질이 좋냐는 것이 아니라, Hyperreal과 같은 실수 체계가 아닌 곳에서도 수학을 할 수 있다는 점입니다. 왜 수학에서 이 이야기는 존재하려고 하는가? ] J dilla - Flyyyyyy 성질이 없는 곳에서도 이야기가 있다. 성질이 없는 곳에 이야기를 만든다. 그것은 까다롭고 지저분하다 못해 끔찍한 수준이다. 비춰지는 실재를, 연속적인 관념을 거부하며 목표도 의미도 없는 것처럼 성질이 없는 곳을 배회한다. 왜 수학은 없는 존재에 있어 존재하려고 하는가? 해석학이 자주 언급되었던 이유는 해석학이야말로 절대적인 예이기 때문일 것이다. 해석학이 있기 전까지는 중간값의 정리를 공리처럼 두기도 했다. 중간값의 정리의 자명함을 거부함으로서 해석학은 시작되었다. 증명은 훨씬 더 길어지고, 해석학은 훨씬 더 까다로워졌다. 그 수많은 well-behaved한 해석학의 정리 앞에서 디리클레 함수를 제시하는 것을 전혀 거부하지 않는 이유가 무엇인가. 바이어슈트라스 함수의 그 성질에도 존재에 의문을 가지지 않은 이유가 무엇인가. 코시는 더 진지하게 생각했어야 했다. 코시를 쓴 것은 Complete가 아니다. 코시를 세 번 쓴 것, 그보다 더 많이 쓴 무한한 존재들과 차이가 전혀 없게 되었다. 해석학이 아닌 대수학도 이러하다. field를 정의함으로서 유리수에 적용되는 많은 성질들을 거부했다. 유리수와 실수에서 있지도 않은 field만의 정리가 나타났다. 이렇게 field는 p-adic number를 실수와 같은 위치에 두었다. 대수학은 abel을 거부하였다. 당연해 보이던 아벨은 normal처럼 특이해졌다. group만의 이론들과 대상들은, 그러자 다른 분야에선 전혀 존재하지 않은 이야기가 존재하였다. 수학에 괴물이 존재합니다. 기하학에서도, topology에서도 찾을 수 있는 존재이다. 수학은 right half-open interval topology를 만들어냈다. 일반적인 point-set topology 대신에 right half-open interval topology를 실수 위에 구성하고 그것으로 극한을 정의한다면 이 topology는 모든 좌극한의 수렴성을 부정한다. 그 topology로 극한을 정의한다면 0.999...를 수렴조차 못하게 만든다는 것이다. [] 왜 정수론인가. 수학의 주제들 중에서 소수만큼 성질이 안 좋은 것이 있을까. 결코 접근할 수 없는 듯한 끔찍한 한계와 같음에도 손으로 잡으려 든다. 그럼에도 이들은 전부 수학이다. 무엇이 진리인가? 여기 무엇이 "진리" 라는 작태를 부릴 수 있다는 것인가? 다른 구조에 대한 것도 아닌, 하우스도르프 그 자체에 있어서 진리인지 아닌지 말하겠다는 것이 무슨 의미가 있는가? Vacuous이다. 이 모든 이야기에서 어디가 거짓되었다고 말할 수 있는가? ... 수학은 유령을 위한 것이 아니다. 아무런 공식도, 정리도, 이론도 있지 않은 유령에 홀린 사람의 최대한 수학이 아닌 이야기. 무한이 의미가 무엇인지, 무한의 존재가 무엇인지 사유만 하는 것을 수학이라고 할 것인가? ... 하지만 이것에도 부정을 해야 합니다. 이것에도 비판할 것은 존재합니다. 저는 비판을 해야 합니다. 어떤 생각에서인지 유령은 님을 비웃습니다. 유령은 이렇게 말한다. . 그건 너무 정해져 있어요. 고통받고 있습니다. Claim 4의 의미는 "성질성"일 것입니다. 성질이 좋지 않다는 것이, 수학으로 이야기하기에 나쁘다는 것이 실수가 진리임을 밝히는 이유일 수 있나요. "0.999... = 1 에 대해, 0.999...를 S라고 둔다. S = 0.999... 10S = 9.999... 10S - S = 9 9S = 9 S = 1" 성질이 많다는 것이 진리가 될 수 있는 것이라면 이것이 가장 이상적인 대답일 것입니다. 이 intuition이야말로 모든 성질, 사칙연산이 있는 것 아닌가요? [해석학은 무엇을 해석한 것인가요?] 해석학이라고 하는 것도 결국에는 그런 것이 아니었나요. 왜 그렇게 당연한 것에 있어 색조가 없는 이야기만을 만들었나요. 다른 분야에서 쓰이는 정리들을 제대로 적용하기 어려운 것은 증명 방법에 제한이 있어서 더 긴, 더 지저분한 증명으로 대체한 것은 어떤 성질은 그 어떤 방법으로도 다시는 쓰지 못한 것은 오히려 해석학을 향한 이야기가 아니었나요? 성질이 많은 것이 수학을 이끌어 갈 것이라는 맹목적인 관념이 존재했지만, 그 성질의 결과야말로 의존 선택 공리와 선택 공리의 선택이 아니었나요. 같은 방향이 아니지 않았을까요. 심미성이 수학을 결정하지 못하던 고대 그리스의 비판과 같이, well-behaved한 것이, 성질이 좋다는 것이 진리가 될 수는 없습니다. 이것이 이 이야기의 극한일까요. 이것은 도저히 잡지 못할 것인가요. 하지만 방법이 있을 것입니다. 유령을 막을 방법이 있을 것입니다. 판명할 수 없는 이 유령을 막을 것입니다. 가장 처음에 문제가 있었습니다. 이 이야기는 처음에부터 문제가 있던 것입니다. 순백이 있을 것입니다. 의미들이, 수학에 있는 이 모든 의미들이 제한 없이는 존재할 수 없는 이 경계로부터 경계가 없는 절대적인 이야기로 들어가게끔 할 것입니다. 최대의 질서와 그에 따른 다양성으로 이 모든 것이 원하려 했던 완전성을 얻을 것입니다. 그 의미가 전체적인 수학이 아닐 지라도 각각의 의미는 그 자신을 구성하는 것이 무엇인지를 보여줄 것입니다. 이 의미가 모두 모여졌을 때 그 의미가 가지는 연결은 수학의 전체를 보여줄 것입니다. 그렇게, 이 순백에는 창문을 달 수 없을 것입니다. 수학에 존재하는 그 모든 의미들을 찾아낼 수 있을 것입니다. 그리고 그 의미들에서도 그 안의 의미들을 분석하여 그를 찾을 수 없을, 찾는 것이 불필요한 가장 단순한 의미가 있을 것입니다. 이는 infinitesimal이고, 공리가 되고 기호가 될 것입니다. 전혀 대담하지도, 환상적이지도 않은 이 공리들과 기호들은 자신만의 테두리를 가지며 더 이상 어떤 차이도 가지지 않음을 보일 것입니다. 가장 큰 수학이, 가장 기초적인 연결이, 가장 확실한 실체가 될 것입니다. 논리적으로 필요한, 모든 가능세계에서 참이 되는 수학이 될 것입니다. [A formal system is complete if for every statement of the language of the system, either the statement or its negation can be derived (i.e., proved) in the system.] 그 어떤 수학적 명제라고 한들 이들이 쌓아놓은 공간 위에 있을 것입니다. 그렇게 나올 충족이유라는 단어는 완전함과 같습니다. 그리고 이러한 진리가 실재한다면 그 존재는 너무나 현실적이기 때문에 이 수학에 있어 현실적인 어떤 자동기계로 사물의 기초를 둘 수 있을 것입니다. 그 어떤 톱니바퀴보다도 뛰어날 이 수학의 자동기계는 그 infinitesimal에서까지 여전히 기계가 자리잡아 있을 것입니다. 그 기계가 종종 부분적으로 몰락하고 껍질을 벗거나 입을 수는 있겠지만 절대 파괴될 수는 없을 것입니다. 이렇게 제시될 수 있는 것이 수학의 순백입니다. degré zéro. 0. 이것은 논리적이고, 물질적이고, 실체적일 뿐만 아니라, 완전하다. 1. 0.999...가 1인지 1이 아닌지에 대한 대답은 더 이상 남아있지 않다. 그리고 바로 이것이 대답이다. ... ... ...잠시만요. Promise 1. 0.999...가 1인지 1이 아닌지에 있어 물질적이거나, 실체적인 것이 답의 근거가 될 수 없다. ... Promise 1이 전에 있었습니다. ... 괜찮을 거예요. 물질적이고 실체적이지 않아도 지금까지 이야기들처럼 논리적인 기호와 공리로 알 수 있을 거예요. 아마 그럴 거예요. ...  이들의 이야기는 더 이상 비추어지지 않는다. 가까이 가고 있는 그는 유령보다 더 무서운 존재가 있음을 확신한다. 사람들은 거대한 괴물을 보았습니다. 우리 모두는 두려워한다. 우리 자신에 대해. 미래에 대해. 세상에 대해. 그 괴물은 이 이야기를 하던 모든 것들을 다 먹으려 들었다. 유령은 무엇인가 말하려고 하자마자 입 속으로 빨려들어갔다. 근방에 있는 것은 그 괴물의 "마시겠다"라는 굉음뿐이다. 유령은 그 상황에서도 이것이 무슨 과정인지 탈주인지 의미를 찾았다. 신을 입 속에서 탓하지 말아야 했음이다. 유령에게도 강제가 필요할지 몰랐음이다. 그 입엔 세상만큼 큰 세상과 코골이가 있었다. 검은 가죽에 의미가 없는 것과 같이 이 이야기도 그렇다. 그 모두의 앞에 있는 부서진 마스트와 찢어진 돛만이 이 입 속이야말로 강 너머에 태양이 떠오름을 알았다. 이것은 진리이다, 여러분. 나를 용서하라. 내가 당신들의 잘못에 개의치 않는 만큼 내 잘못도 염두에 두지 말기를 바란다. 이 뒤틀림을 본 그는 그 괴물을 두고 팡타그뤼엘이라고 말한다. 그가 춤과 같은 몸짓을 하자 0.999...는 1이 되었다. Au moment du tra vail, quand peu à peu une compréhension s’amorce, prend forme, s’approfondit ; quand dans une confusion peu à peu on voit apparaître un ordre, ou quand ce qui semblait familier soudain prend des aspects insolites, puis troublants, jusqu’à ce qu’une contradiction enfin éclate et boule verse une vision des choses qui paraissait immuable - dans un tel tra vail, il n’y a trace d’ambition, ou de vanité. Ce qui mène alors la danse est quelque chose qui vient de beaucoup plus loin que le "moi" et sa fringale de s’agrandir sans cesse (fut-ce de "sa voir" et de "connaissances") - de beaucoup plus loin sûrement que notre personne ou même notre espèce. C’est là la source, qui est en chacun de nous. - Récoltes et Semailles 중에서 - 16
|
|