- 회원들이 추천해주신 좋은 글들을 따로 모아놓는 공간입니다.
- 추천글은 매주 자문단의 투표로 선정됩니다.
| Date | 17/04/15 00:58:59 |
| Name | 캡틴아메리카 |
| Subject | 음수X음수는 왜 양수인가요? |
|
[음수X음수는 왜 양수인가요?] 아이들에 수학을 가르치다 보면 거의 100%의 아이들이 선생님께 꼭 물어보게 되는 질문이라고 합니다. 최근에 아이들에게 수학을 가르치는 선생님인 한 지인이 저에게 이런 질문을 자주 받는데 명쾌하게 설명하는 방법이 없냐고 그러더군요. [정의상 그렇게 정의하는 것이 수학에서 가장 자연스러운 정의이다.] 같은 답 말고 현실적으로 아이들을 쉽게 이해시킬만 한 답이 없냐고요. 저에게는 아주 짧고도 명쾌한 답이 있습니다. [빚이] [나갔으니까요.] 하지만, 이렇게 이야기를 해도 한 번에 이해가 되는 사람은 많이 없을 겁니다. 그런데 제 답변에서 특이한 걸 발견하지 않으셨나요? 왜 [빚이 나갔으니까요.]로 []를 1번만 쓰지 않고, [빚이] [나갔으니까요.]로 []를 2개로 분리해서 답을 했을까요? 이 답을 이해하려면 [두 가지]를 다시 한 번 명쾌하게 이해하셔야 합니다. 첫번째, [우선 곱셈이란 것이 무엇인지 제대로 이해해야 합니다.] (먼저 몇 년 전 옆동네를 뜨겁게 달궜던 다음 글을 참고해 보세요. http://pgr21.com/?b=10&n=176684 ) [2X3과 3X2는 둘 다 6이니까 같은 것이 아니냐]라고 생각하시는 분들이 많을 겁니다. 물론 예상하셨겠지만, 제 답은 [아니오]입니다. 2X3는 2가 3번 있는 것이고, 3X2는 3이 2번 있는 것이죠. 수학은 결과 뿐만 아니라, [과정이 매우 중요한 학문]이라는 것은 누구나 아실 겁니다. 2가 3번 있는 것과 3이 2번 있는 것은 [그 과정이 매우 다른 것이죠.] 한국 사람들은 돈 문제를 가지고 다루면 더 명확하게 이해한다고 하니 돈으로 설명 해보겠습니다. 아이가 부모님께 한 달 용돈을 2만원을 받는다고 합시다. 아이가 용돈을 3달 동안 받았습니다. 그러면 아이가 3달 동안 받은 총 용돈은 2X3=6만원이죠. 하지만, 3X2는 그 내용이 달라요. 이것은 한 달 용돈이 3만원이고, 그런 용돈을 2달간 받은 것입니다. 2X3과 3X2의 결과는 모두 6이지만, 그 과정은 명백히 다른 것이에요. 두번째, [음수가 무엇인지 이해하셔야 합니다.] 역시나 돈 문제를 가지고 설명해보죠. 흔히들 돈을 가지고 있는 것을 양수라고 한다면, [빚을 가지고 있는 것을 음수라고 한다]고 생각하실 겁니다. [땡! 틀렸습니다.] 사실 좀 더 정확하게 말하면, [반은 맞고 반은 틀렸습니다.] 음수는 [빚]만 음수인게 아닙니다. 돈이 [나간 것]도 음수입니다. 곱셈으로 설명해보겠습니다. (-2)X3은 아이가 한 달 용돈을 받지 못 해 친구한테 빌려서 [빚이 2만원]인데, 그러한 빚이 [3달 동안 생긴 것이죠.] 2X(-3)은 아이가 한 달 동안 [용돈 2만원]을 받는데, [3달 동안 써버린 것입니다.] 즉, 하나는 [6만원의 빚]이 생긴 것, 다른 하나는 수중에서 [6만원이 나간 것]이에요. 그렇다면 음수X음수는 왜 양수? 위에서 배운 것을 종합해보면 답을 금방 알 수 있습니다. 2X3 = 6 <- 2만원의 [돈이] 3번 [들어온 것], 그래서 6만원의 [돈이] [들어온 것] 3X2 = 6 <- 3만원의 [돈이] 2번 [들어온 것], 그래서 6만원의 [돈이] [들어온 것] (-2)X3 = -6 <- 2만원의 [빚이] 3번 [들어온 것], 그래서 6만원의 [빚이] [들어온 것] 2X(-3) = -6 <- 2만원의 [돈이] 3번 [나간 것], 그래서 6만원의 [돈이] [나간 것] 그렇다면 자연스럽게 다음 답이 나오실 겁니다. (-2)X(-3) = 6 <- 2만원의 [빚이] 3번 [나간 것], 그래서 6만원의 [빚이] [나간 것] = 따라서 결과적으로 6만원의 [돈이] [들어온 것] 이제 여러분들도 아이들이 음수X음수는 왜 양수냐고 질문이 오면 자신있게 [빚이] [나갔으니까]라고 답해주시면 됩니다. :) p.s. 수학도 과학이니 과학 카테고리가 맞겠죠? ㅋㅋ * 수박이두통에게보린님에 의해서 티타임 게시판으로부터 게시물 복사되었습니다 (2017-04-24 08:06) * 관리사유 : 추천 게시판으로 복사합니다. 14
|
|
중학생 때 잠깐 다녔던 학원에서 울었던 적이 있어요. 수학 시간이었는데요, 음수를 배웠는데요. 다른 애들은 다 이해를 하는데, 저만 못하는 것 같더라고요. '0보다 작은데 어떻게 더하고 뺀다는 거야? 1개도 없는 건데??' 그게 너무 분해서 -.-... 막 혼자 눈물 흘리고 있으니까 다른 이들은 이해를 못해서 왜 우냐고, 좀 심하게 말하는 이는 관심 받으려 그러냐고. 물론 지금은 좀 커서 남 앞에서 울지는 않고, 또 제 이해의 한계가 어디인지도 어렴풋이 감이 오니 대학 시절 수업을 들으며 공미방 이해를 못하는 게 심히 분하진 않았지만 그때는 그랬어요. 지금 생각해 보면 그때 다른 친구들도 이렇게 이해를 했다기보다는 그냥 넘어간 아이들이 다수일 것 같아요. 수학도 제가 이해하는 영역까지는 재미있습니다. 이 글처럼요. 냠냠...
인공지능에 대해 연구하는 분이 쓴 글에서 본 것으로 기억하는데 딥러닝이 대체 어떻게 작동하는지에 대해 연구한 글이었던 것 같네요.
그런데 그 글에서 공리에 대해 연구하던 수학자(???)가 '수학이나 논리학 따위에서 증명이 없이 자명한 진리로 인정되는 원리'는 존재할 수 없다는 결론을 내렸다는 내용을 본 기억이 나서 적어봤습니다.
그런데 절대적 논리 체계는 아니어도 상대적 논리 체계 구축은 가능하고 그 상대적 논리 체계 하에서 만들어진 것이 컴퓨터인 것처럼 딥러닝류에 이뤄지는 학습 역시 상대적 논리 체계가 형성되기 때문이라는 주장이었던 것으로 기억합니다.
문송한 사람이라서 이렇게 투박하게 밖에 표현하지 못하겠네요. ^^;
그런데 그 글에서 공리에 대해 연구하던 수학자(???)가 '수학이나 논리학 따위에서 증명이 없이 자명한 진리로 인정되는 원리'는 존재할 수 없다는 결론을 내렸다는 내용을 본 기억이 나서 적어봤습니다.
그런데 절대적 논리 체계는 아니어도 상대적 논리 체계 구축은 가능하고 그 상대적 논리 체계 하에서 만들어진 것이 컴퓨터인 것처럼 딥러닝류에 이뤄지는 학습 역시 상대적 논리 체계가 형성되기 때문이라는 주장이었던 것으로 기억합니다.
문송한 사람이라서 이렇게 투박하게 밖에 표현하지 못하겠네요. ^^;
http://www.pgr21.com/pb/pb.php?id=freedom&no=70685&divpage=14&sc=on&keyword=%EC%97%B0%EC%97%AD%EB%A1%A0
이 글에 있는 링크로 가서 딥러닝 관련 글을 보다가 나왔습니다.
그런데 지금 확인해 보니 그 링크로 연결이 안 되네요.
구글에서 '이기준 연역론'으로 검색해 봐도 찾기 힘들고요.
이기준이라는 사람이 공리에 대해 이야기한 게 아니라 이기준이라는 사람이 딥러닝의 상대적 논리 체계에 대해 설명하는 과정에서 언급되었는데 그 학자가 상당히 공신력이 있는 사람으로 기억합니다.
처음 들어보는 사람이라 기억은 못하지만... ^^;
이 글에 있는 링크로 가서 딥러닝 관련 글을 보다가 나왔습니다.
그런데 지금 확인해 보니 그 링크로 연결이 안 되네요.
구글에서 '이기준 연역론'으로 검색해 봐도 찾기 힘들고요.
이기준이라는 사람이 공리에 대해 이야기한 게 아니라 이기준이라는 사람이 딥러닝의 상대적 논리 체계에 대해 설명하는 과정에서 언급되었는데 그 학자가 상당히 공신력이 있는 사람으로 기억합니다.
처음 들어보는 사람이라 기억은 못하지만... ^^;
가서 말씀하신 공리가 언급된 부분을 읽었는데,
공리가 무엇인지 잘 모르는 사람이 공리에 대해 논했네요.
딥러닝에는 공신력이 있는 사람일지는 몰라도 [수학적 기초론은 전혀 모르는 사람]같군요.
공리 언급 부분은 시작부터 잘못된 이야기를 하고 있습니다.
공리는 애초에 절대적인 것이 아닌데,
절대적인 것으로 생각하고 논의를 펴고 있으니 말도 안되는 소리를 할 수 밖에요.
또한, 수학계에서 "공리를 가정해보자"고 주장한다고 했는데 그것도 틀렸네요.
공리는
공리가 무엇인지 잘 모르는 사람이 공리에 대해 논했네요.
딥러닝에는 공신력이 있는 사람일지는 몰라도 [수학적 기초론은 전혀 모르는 사람]같군요.
공리 언급 부분은 시작부터 잘못된 이야기를 하고 있습니다.
공리는 애초에 절대적인 것이 아닌데,
절대적인 것으로 생각하고 논의를 펴고 있으니 말도 안되는 소리를 할 수 밖에요.
또한, 수학계에서 "공리를 가정해보자"고 주장한다고 했는데 그것도 틀렸네요.
공리는
가서 말씀하신 공리가 언급된 부분을 읽었는데,
공리가 무엇인지 잘 모르는 사람이 공리에 대해 논했네요.
딥러닝에는 공신력이 있는 사람일지는 몰라도 [수학적 기초론은 전혀 모르는 사람]같군요.
공리 언급 부분은 시작부터 잘못된 이야기를 하고 있습니다.
공리는 애초에 절대적인 것이 아닌데,
절대적인 것으로 생각하고 논의를 펴고 있으니 말도 안되는 소리를 할 수 밖에요.
또한, 수학계에서 "공리를 가정해보자"고 주장한다고 했는데 그것도 틀렸네요.
공리는 [기호(taste)의 문제], 즉, 내가 원하면 받아들이고, 원하지 않으면 받아들이지 않아도 되는 것입니다.
현재 주류 수학계에서 받아들이고 있는 공리계(ZFC)가 있고, 그걸 대부분의 수학자가 원해서 받아들이는 것이지,
그것을 절대적인 것으로 생각하는 수학자는 없다고 봅니다.
공리가 무엇인지 잘 모르는 사람이 공리에 대해 논했네요.
딥러닝에는 공신력이 있는 사람일지는 몰라도 [수학적 기초론은 전혀 모르는 사람]같군요.
공리 언급 부분은 시작부터 잘못된 이야기를 하고 있습니다.
공리는 애초에 절대적인 것이 아닌데,
절대적인 것으로 생각하고 논의를 펴고 있으니 말도 안되는 소리를 할 수 밖에요.
또한, 수학계에서 "공리를 가정해보자"고 주장한다고 했는데 그것도 틀렸네요.
공리는 [기호(taste)의 문제], 즉, 내가 원하면 받아들이고, 원하지 않으면 받아들이지 않아도 되는 것입니다.
현재 주류 수학계에서 받아들이고 있는 공리계(ZFC)가 있고, 그걸 대부분의 수학자가 원해서 받아들이는 것이지,
그것을 절대적인 것으로 생각하는 수학자는 없다고 봅니다.
'두 점이 주어졌을 때, 그 두 점을 통과하는 직선을 그을 수 있다.'
이런 대표적인 유클리드 기하의 공리가 없다는 게 증명된 적이 있다는 소리는 처음들었습니다. 혹시 관련 논문이나 기사라도 알 수 있을까요?
그리고 공리는 증명없이 자명한 진리로 인정되는 원리라기보다 소급하다보면 더 이상 증명하기 어려운 기초적인 근거들을 말합니다. 우리는 어떤 명제를 증명하기 위해 근거들을 계속 해체해나가는데 어느 순간에는 해체할 수 없는 수준이 오게 됩니다. 그런 근거들은 결국 실증적 증거에 의존할 수 밖에 없게 되죠. 유클리드 공간의 극... 더 보기
이런 대표적인 유클리드 기하의 공리가 없다는 게 증명된 적이 있다는 소리는 처음들었습니다. 혹시 관련 논문이나 기사라도 알 수 있을까요?
그리고 공리는 증명없이 자명한 진리로 인정되는 원리라기보다 소급하다보면 더 이상 증명하기 어려운 기초적인 근거들을 말합니다. 우리는 어떤 명제를 증명하기 위해 근거들을 계속 해체해나가는데 어느 순간에는 해체할 수 없는 수준이 오게 됩니다. 그런 근거들은 결국 실증적 증거에 의존할 수 밖에 없게 되죠. 유클리드 공간의 극... 더 보기
'두 점이 주어졌을 때, 그 두 점을 통과하는 직선을 그을 수 있다.'
이런 대표적인 유클리드 기하의 공리가 없다는 게 증명된 적이 있다는 소리는 처음들었습니다. 혹시 관련 논문이나 기사라도 알 수 있을까요?
그리고 공리는 증명없이 자명한 진리로 인정되는 원리라기보다 소급하다보면 더 이상 증명하기 어려운 기초적인 근거들을 말합니다. 우리는 어떤 명제를 증명하기 위해 근거들을 계속 해체해나가는데 어느 순간에는 해체할 수 없는 수준이 오게 됩니다. 그런 근거들은 결국 실증적 증거에 의존할 수 밖에 없게 되죠. 유클리드 공간의 극좌표계에서 두 점이 주어졌을 때 직선을 그을 수 있다는 공리를 바탕으로 수 많은 기하적 이론들을 증명하게 되는데, 정작 그 기하적 이론의 토대가 되는 근거를 증명하는 수준에는 한계가 있다는 것이죠. 이러한 공리는 비단 수학뿐만이 아니라 다른 학문에도 존재합니다. 뉴턴역학만 하더라도 '힘'이나 '관성'이 있다고 가정하고 그걸 공준으로 삼아 증명해나가는데 뉴턴 본인은 그런 힘과 관성의 존재를 논리적으로 증명하진 못했어요.
그리고 바로 그러하기에 그러한 공준을 따르지 않는 학문체계도 가능합니다. 비유클리드적 공간에서의 수학도 존재하고 해밀턴 역학이 있죠. 어찌되었든 공리란 대부분 어떤 학문의 근거를 만들기 위한 최소한의 가정이라서 '공리가 없다는게 증명되었다.' 이 말은 사실이냐 아니냐를 따지기 이전에 좀 어폐가 있습니다. 저런 문장이 성립하는 상황이 어떻게 있는 지 잘 모르겠어요.
이런 대표적인 유클리드 기하의 공리가 없다는 게 증명된 적이 있다는 소리는 처음들었습니다. 혹시 관련 논문이나 기사라도 알 수 있을까요?
그리고 공리는 증명없이 자명한 진리로 인정되는 원리라기보다 소급하다보면 더 이상 증명하기 어려운 기초적인 근거들을 말합니다. 우리는 어떤 명제를 증명하기 위해 근거들을 계속 해체해나가는데 어느 순간에는 해체할 수 없는 수준이 오게 됩니다. 그런 근거들은 결국 실증적 증거에 의존할 수 밖에 없게 되죠. 유클리드 공간의 극좌표계에서 두 점이 주어졌을 때 직선을 그을 수 있다는 공리를 바탕으로 수 많은 기하적 이론들을 증명하게 되는데, 정작 그 기하적 이론의 토대가 되는 근거를 증명하는 수준에는 한계가 있다는 것이죠. 이러한 공리는 비단 수학뿐만이 아니라 다른 학문에도 존재합니다. 뉴턴역학만 하더라도 '힘'이나 '관성'이 있다고 가정하고 그걸 공준으로 삼아 증명해나가는데 뉴턴 본인은 그런 힘과 관성의 존재를 논리적으로 증명하진 못했어요.
그리고 바로 그러하기에 그러한 공준을 따르지 않는 학문체계도 가능합니다. 비유클리드적 공간에서의 수학도 존재하고 해밀턴 역학이 있죠. 어찌되었든 공리란 대부분 어떤 학문의 근거를 만들기 위한 최소한의 가정이라서 '공리가 없다는게 증명되었다.' 이 말은 사실이냐 아니냐를 따지기 이전에 좀 어폐가 있습니다. 저런 문장이 성립하는 상황이 어떻게 있는 지 잘 모르겠어요.
이거 이해 못하면 머리 나쁜 걸까요.
빚은 '지다' '탕감받다'라고 표현 하잖아요. 그래서 저는 직관적으로 안 와 닿아요 ㅠ
Patterns
Here's a plausibility argument drawn from multiplication patterns:
3 x -3 = -9
2 x -3 = -6
1 x -3 = -3
0 x -3 = 0
-1 x -3 = 3
저는 이게 제일 이해가 잘 됐어요. 물리법칙이 존재하... 더 보기
빚은 '지다' '탕감받다'라고 표현 하잖아요. 그래서 저는 직관적으로 안 와 닿아요 ㅠ
Patterns
Here's a plausibility argument drawn from multiplication patterns:
3 x -3 = -9
2 x -3 = -6
1 x -3 = -3
0 x -3 = 0
-1 x -3 = 3
저는 이게 제일 이해가 잘 됐어요. 물리법칙이 존재하... 더 보기
이거 이해 못하면 머리 나쁜 걸까요.
빚은 '지다' '탕감받다'라고 표현 하잖아요. 그래서 저는 직관적으로 안 와 닿아요 ㅠ
Patterns
Here's a plausibility argument drawn from multiplication patterns:
3 x -3 = -9
2 x -3 = -6
1 x -3 = -3
0 x -3 = 0
-1 x -3 = 3
저는 이게 제일 이해가 잘 됐어요. 물리법칙이 존재하지만 왜 존재하는지는 모르듯이 숫자도 다음과 같은 패턴이 존재할 뿐이라고 이해. 이해되는 예들이 많지만 그 예에 한정되는 느낌일 뿐 음수와 양수를 관념적으로 떠올렸을 때 (-3) x (-3)은 직관적인 이해가 어려워요. 그래서 저는 아이들이 음수, 양수를 어려워하는 게 무척 공감이 갔어요.
빚은 '지다' '탕감받다'라고 표현 하잖아요. 그래서 저는 직관적으로 안 와 닿아요 ㅠ
Patterns
Here's a plausibility argument drawn from multiplication patterns:
3 x -3 = -9
2 x -3 = -6
1 x -3 = -3
0 x -3 = 0
-1 x -3 = 3
저는 이게 제일 이해가 잘 됐어요. 물리법칙이 존재하지만 왜 존재하는지는 모르듯이 숫자도 다음과 같은 패턴이 존재할 뿐이라고 이해. 이해되는 예들이 많지만 그 예에 한정되는 느낌일 뿐 음수와 양수를 관념적으로 떠올렸을 때 (-3) x (-3)은 직관적인 이해가 어려워요. 그래서 저는 아이들이 음수, 양수를 어려워하는 게 무척 공감이 갔어요.
저도 그게 이해가 안되었어요. 음수라는 표현 자체가 어색하고 낯설었으니까요. 그래서 질문해봐도 "그건 우리가 그러기로 약속한거야. 그냥 그렇게 외우렴" 하고 답하셨던지라. 그러나 호기심이 많았던 저는 인터넷의 힘을 빌렸고 당연히 이해가 안되었기에(...) 그냥 저만의 표현을 만들었어요.
3 x 2 =6 이라는 기본적인 곱셈 계산 후
-가 0개면 아무것도 없으니 +
-가 1개 있으면 외로운 곱셈이니까 -
-가 2개 있으면 외로운 애랑 외로운애가 만나서 외롭지 않은 곱셈이니까 +.
라는 규칙을 깔고서 이런식으로 저스... 더 보기
3 x 2 =6 이라는 기본적인 곱셈 계산 후
-가 0개면 아무것도 없으니 +
-가 1개 있으면 외로운 곱셈이니까 -
-가 2개 있으면 외로운 애랑 외로운애가 만나서 외롭지 않은 곱셈이니까 +.
라는 규칙을 깔고서 이런식으로 저스... 더 보기
저도 그게 이해가 안되었어요. 음수라는 표현 자체가 어색하고 낯설었으니까요. 그래서 질문해봐도 "그건 우리가 그러기로 약속한거야. 그냥 그렇게 외우렴" 하고 답하셨던지라. 그러나 호기심이 많았던 저는 인터넷의 힘을 빌렸고 당연히 이해가 안되었기에(...) 그냥 저만의 표현을 만들었어요.
3 x 2 =6 이라는 기본적인 곱셈 계산 후
-가 0개면 아무것도 없으니 +
-가 1개 있으면 외로운 곱셈이니까 -
-가 2개 있으면 외로운 애랑 외로운애가 만나서 외롭지 않은 곱셈이니까 +.
라는 규칙을 깔고서 이런식으로 저스스로 이해시켰어요. 당시 저는 -는 부정적인거, +는 긍정적이라는 느낌을 받았어요. 외로움은 부정적인것이니까. 이렇게 보니 이게 더 복잡한 것 같아요(...)
시간이 좀 흐르고 외로움이 꼭 부정적인것만은 아니란걸 알게되었지만 그래도 이 규칙은 변함없네요.
그 때는 닥치고 외워, 라는 공부가 이해안되었어요. 증명을 해내야만 아하!하고 익히는지라...이해가 안되는데 쓸 수가 없었기에 저런 억지를 부려가면서 이해 시키려했던게 생각나네요. 캡틴아메리카님이 제시하신 방법도 좋은것같아요ㅎㅎ 저런식으로 생각해본 적 없는데 꽤 괜찮은것같아요.
3 x 2 =6 이라는 기본적인 곱셈 계산 후
-가 0개면 아무것도 없으니 +
-가 1개 있으면 외로운 곱셈이니까 -
-가 2개 있으면 외로운 애랑 외로운애가 만나서 외롭지 않은 곱셈이니까 +.
라는 규칙을 깔고서 이런식으로 저스스로 이해시켰어요. 당시 저는 -는 부정적인거, +는 긍정적이라는 느낌을 받았어요. 외로움은 부정적인것이니까. 이렇게 보니 이게 더 복잡한 것 같아요(...)
시간이 좀 흐르고 외로움이 꼭 부정적인것만은 아니란걸 알게되었지만 그래도 이 규칙은 변함없네요.
그 때는 닥치고 외워, 라는 공부가 이해안되었어요. 증명을 해내야만 아하!하고 익히는지라...이해가 안되는데 쓸 수가 없었기에 저런 억지를 부려가면서 이해 시키려했던게 생각나네요. 캡틴아메리카님이 제시하신 방법도 좋은것같아요ㅎㅎ 저런식으로 생각해본 적 없는데 꽤 괜찮은것같아요.
영어와 우리말의 차이가 있는데 영어권에서는 3 times 5 라고 하면 5+5+5 라고 가르치는 것 같습니다. 아시는 분은 답변 좀..
https://medium.com/i-math/why-5-x-3-5-5-5-was-marked-wrong-b34607a5b74c
https://medium.com/i-math/why-5-x-3-5-5-5-was-marked-wrong-b34607a5b74c
(음수와 양수의) 사칙연산에서의 핵심은
(하나). [ + (-3) = - (+3) ], [ - (-3) = + (+3) ]는 등식 양팔저울에서 보면 직감적으로 이해.
https://draft.blogger.com/blog/post/edit/6807701986403764511/4252232388930450128... 더 보기
(하나). [ + (-3) = - (+3) ], [ - (-3) = + (+3) ]는 등식 양팔저울에서 보면 직감적으로 이해.
https://draft.blogger.com/blog/post/edit/6807701986403764511/4252232388930450128... 더 보기
(음수와 양수의) 사칙연산에서의 핵심은
(하나). [ + (-3) = - (+3) ], [ - (-3) = + (+3) ]는 등식 양팔저울에서 보면 직감적으로 이해.
https://draft.blogger.com/blog/post/edit/6807701986403764511/4252232388930450128
(둘).
[ 3 - 5 = - 2 ] = [ 재산3 – 재산5 = - 재산2 ] : ‘재산’을 빼도 계산에는 영향이 없습니다.
[ 3 - 5 = - 2 ] = [ 재산3 + 빚5 = + 빚2 ] :
[ 3 – 5 = - 2 ] = [ 3 + 빚5 = + 빚2 ] : ‘재산’을 빼도 계산에는 영향이 없습니다.
[ 3 – 5 = - 2 ] = [ 3 + 빚5 = 빚2 ] : (+)를 빼도 계산에는 영향이 없습니다.
[ - 2 ] = [ 빚2 ]
[ 빼다 2 ] = [ 빚2 ]
[ 빼다 2 ] = (-2) = [ 빚2 ] ~> [ - 2 ] = (-2) = [ 음2 ]
결국 [ 작은수 – 큰수 = - 수 = -수 = 음수 ]
( [ 빼다 2 ] = (-2) )에 (더하다)로 바꾸어 두면 ( [ 더하다 2 ] = (+2) = (재산2) = (양2) )
(셋). (음수와 양수)의 덧셈과 뺄셈은 상계[=엇셈]한 나머지가 정답입니다.
(넷). (-3) = (-3) = (-3)
+ (-3) = (-3) = + (-3)
+ (-3) = (-3) = - (+3)
+(-3) = (-3) = -(+3)
(+1)(-3) = (-3) = (-1)(+3)
(+1)(-3) = (-3) = (-1)(3)
(+1)(-3) = (-3) = -(1)(3)
(+1)(-3) = (-3) = -(1*3)
(+1)(-3) = (-3) = - (1*3)
(+1)(-3) = (-3) = - ( (+1)*3) :: 여기에서 곱셈과 나눗셈의 기호변환은 마감됩니다.
(-6)/(-2) = (-6) * (-0.5) = - ( (-6)* (0.5) ) = - ( (-6)/(2) ) = - ( -3) = + (+3) = 3
(다섯). 음수이해의 어려움을 없애서, 음수를 사용하는 데카르트좌표의 이해, 허수를 사용하는 복소평면과 오일러등식의 이해를 넘어서 푸리에급수 보기까지입니다.
위의 (하나) (둘) (셋) (넷) (다섯)을 염두에 두고 가벼운 마음으로 속전속결하는 것도 좋아 보입니다.
치환법 ( Principles of Mathematical Analysis by Walter Rudin )
(-1)*(3) = -(3) = -3
(-1)*(-3) = -(-3) = - (-3) = + (+3) = (+3) = (3) = 3
문제는, 어짜피 3은 배수의 개념이고, (-3)의 음수기호(-)의 역할이 정확히 파악이 안됨.
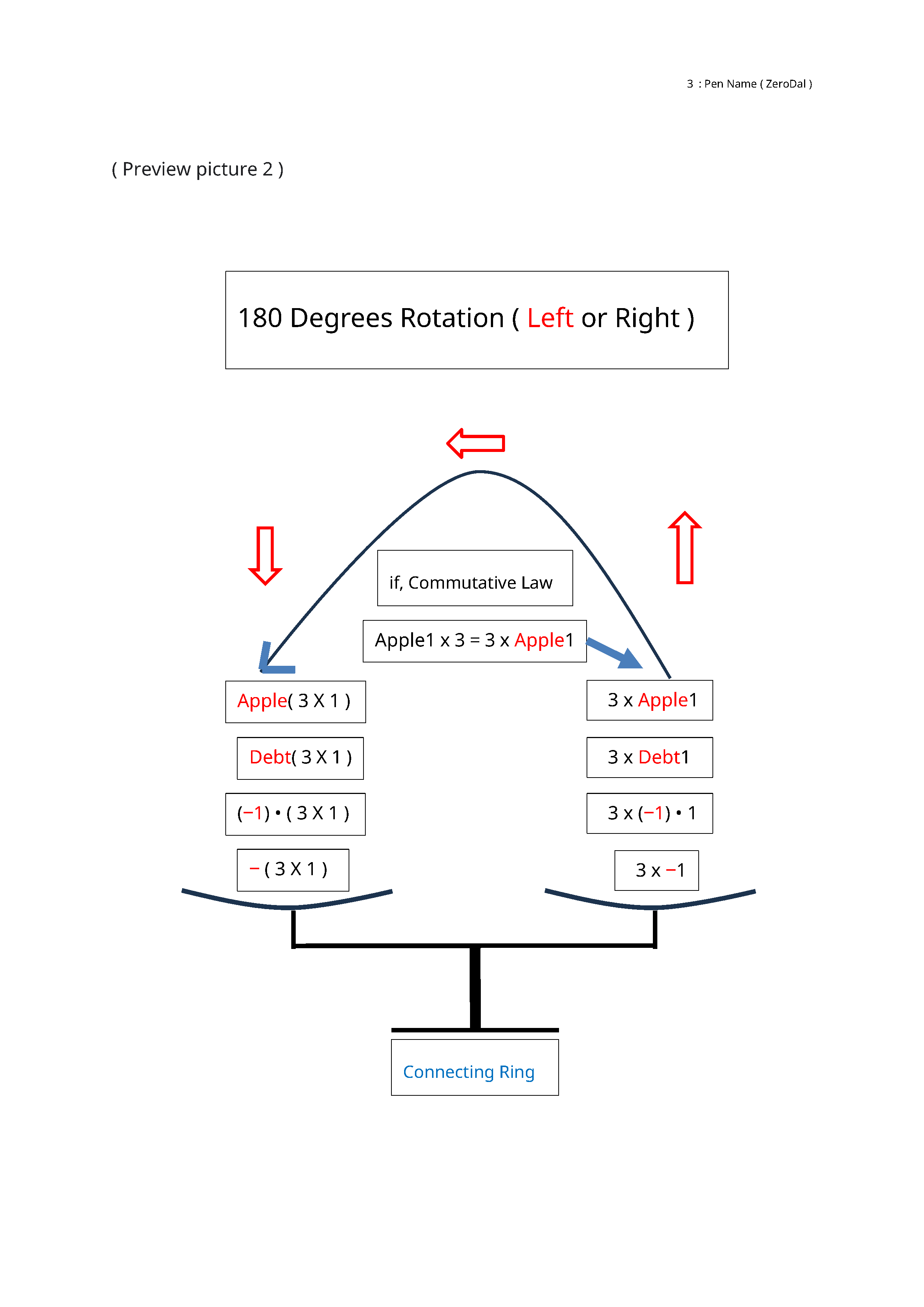
(-3)의 음수기호(-)의 역할은 아래의 그림을 보시면 됩니다.
https://www.zerodal.com/2023/11/303-only-8pages-does-negative-times.html
결국
(-2) x (-3) = (-2)*(-3) = (-2)(-3) = -( (-2) x 3 ) = - ( (-2) x 3 ) = - (-6) = + (+6) = 6
위의 뜻은 [ (채무, 빚2원)을 3배로 곱한 것 ]을 빼다 ~> 채무감소
(+2) x (+3) = + ( (+2) x 3 ) = [ (채권, 돈2원)을 3배로 곱한 것 ]을 더하다 ~> 채권증가
[ 채무감소 = 채권증가 ] * 채권법의 채권소멸의 하나인 상계(=엇셈, 셈셈이, 퉁치기)에서
상계는 기본적으로 양방향성 또는 쌍뱡향성을 가지는데
수직선에서 설명이 쉽지 않습니다. 이유는
1. 음의 수직선 ( 채무증가 0 채무감소 ) : (-2) - (-3)
2. 양의 수직선 ( 채권감소 0 채권증가 ) : (+2) - (+3)
3. 음양의 수직선 ( 채무증가 0 채권증가 ) : (+2) - (-3), (+2) + (-3)
4. 수직선 ( Number Line ) ( 채무증가 0 채권증가 )에서 plus 기호 생략
(하나). [ + (-3) = - (+3) ], [ - (-3) = + (+3) ]는 등식 양팔저울에서 보면 직감적으로 이해.
https://draft.blogger.com/blog/post/edit/6807701986403764511/4252232388930450128
(둘).
[ 3 - 5 = - 2 ] = [ 재산3 – 재산5 = - 재산2 ] : ‘재산’을 빼도 계산에는 영향이 없습니다.
[ 3 - 5 = - 2 ] = [ 재산3 + 빚5 = + 빚2 ] :
[ 3 – 5 = - 2 ] = [ 3 + 빚5 = + 빚2 ] : ‘재산’을 빼도 계산에는 영향이 없습니다.
[ 3 – 5 = - 2 ] = [ 3 + 빚5 = 빚2 ] : (+)를 빼도 계산에는 영향이 없습니다.
[ - 2 ] = [ 빚2 ]
[ 빼다 2 ] = [ 빚2 ]
[ 빼다 2 ] = (-2) = [ 빚2 ] ~> [ - 2 ] = (-2) = [ 음2 ]
결국 [ 작은수 – 큰수 = - 수 = -수 = 음수 ]
( [ 빼다 2 ] = (-2) )에 (더하다)로 바꾸어 두면 ( [ 더하다 2 ] = (+2) = (재산2) = (양2) )
(셋). (음수와 양수)의 덧셈과 뺄셈은 상계[=엇셈]한 나머지가 정답입니다.
(넷). (-3) = (-3) = (-3)
+ (-3) = (-3) = + (-3)
+ (-3) = (-3) = - (+3)
+(-3) = (-3) = -(+3)
(+1)(-3) = (-3) = (-1)(+3)
(+1)(-3) = (-3) = (-1)(3)
(+1)(-3) = (-3) = -(1)(3)
(+1)(-3) = (-3) = -(1*3)
(+1)(-3) = (-3) = - (1*3)
(+1)(-3) = (-3) = - ( (+1)*3) :: 여기에서 곱셈과 나눗셈의 기호변환은 마감됩니다.
(-6)/(-2) = (-6) * (-0.5) = - ( (-6)* (0.5) ) = - ( (-6)/(2) ) = - ( -3) = + (+3) = 3
(다섯). 음수이해의 어려움을 없애서, 음수를 사용하는 데카르트좌표의 이해, 허수를 사용하는 복소평면과 오일러등식의 이해를 넘어서 푸리에급수 보기까지입니다.
위의 (하나) (둘) (셋) (넷) (다섯)을 염두에 두고 가벼운 마음으로 속전속결하는 것도 좋아 보입니다.
치환법 ( Principles of Mathematical Analysis by Walter Rudin )
(-1)*(3) = -(3) = -3
(-1)*(-3) = -(-3) = - (-3) = + (+3) = (+3) = (3) = 3
문제는, 어짜피 3은 배수의 개념이고, (-3)의 음수기호(-)의 역할이 정확히 파악이 안됨.
(-3)의 음수기호(-)의 역할은 아래의 그림을 보시면 됩니다.
https://www.zerodal.com/2023/11/303-only-8pages-does-negative-times.html
결국
(-2) x (-3) = (-2)*(-3) = (-2)(-3) = -( (-2) x 3 ) = - ( (-2) x 3 ) = - (-6) = + (+6) = 6
위의 뜻은 [ (채무, 빚2원)을 3배로 곱한 것 ]을 빼다 ~> 채무감소
(+2) x (+3) = + ( (+2) x 3 ) = [ (채권, 돈2원)을 3배로 곱한 것 ]을 더하다 ~> 채권증가
[ 채무감소 = 채권증가 ] * 채권법의 채권소멸의 하나인 상계(=엇셈, 셈셈이, 퉁치기)에서
상계는 기본적으로 양방향성 또는 쌍뱡향성을 가지는데
수직선에서 설명이 쉽지 않습니다. 이유는
1. 음의 수직선 ( 채무증가 0 채무감소 ) : (-2) - (-3)
2. 양의 수직선 ( 채권감소 0 채권증가 ) : (+2) - (+3)
3. 음양의 수직선 ( 채무증가 0 채권증가 ) : (+2) - (-3), (+2) + (-3)
4. 수직선 ( Number Line ) ( 채무증가 0 채권증가 )에서 plus 기호 생략
잘못된 하이퍼링크 수정 및 추가 내용입니다.
(－3) ＝ (－3) ＝ (－3)
＋ (－3) ＝ (－3) ＝ ＋ (－3)
＋ (－3) ＝ (－3) ＝ － (＋3)
＋ (＋(－3)) ＝ (－3) ＝ － (＋(＋3)) * (－3)
＋ (＋(－3)) ＝ (－3) ＝ ＋ (－(＋3))
(＋(－3)) ＝ (－3) ＝ (－(＋3))
＋(－3) ＝ (－3) ＝ －(＋3)
(＋1) × (－3) ＝ (－3) ＝ (－1) × (3)
(＋1) • (－3) ＝ (－3) ＝ (－1) • (＋3)
(1) • (－3) ＝ (－3) ＝ (－1) • (3)
[－1] • (... 더 보기
(－3) ＝ (－3) ＝ (－3)
＋ (－3) ＝ (－3) ＝ ＋ (－3)
＋ (－3) ＝ (－3) ＝ － (＋3)
＋ (＋(－3)) ＝ (－3) ＝ － (＋(＋3)) * (－3)
＋ (＋(－3)) ＝ (－3) ＝ ＋ (－(＋3))
(＋(－3)) ＝ (－3) ＝ (－(＋3))
＋(－3) ＝ (－3) ＝ －(＋3)
(＋1) × (－3) ＝ (－3) ＝ (－1) × (3)
(＋1) • (－3) ＝ (－3) ＝ (－1) • (＋3)
(1) • (－3) ＝ (－3) ＝ (－1) • (3)
[－1] • (... 더 보기
잘못된 하이퍼링크 수정 및 추가 내용입니다.
(－3) ＝ (－3) ＝ (－3)
＋ (－3) ＝ (－3) ＝ ＋ (－3)
＋ (－3) ＝ (－3) ＝ － (＋3)
＋ (＋(－3)) ＝ (－3) ＝ － (＋(＋3)) * (－3)
＋ (＋(－3)) ＝ (－3) ＝ ＋ (－(＋3))
(＋(－3)) ＝ (－3) ＝ (－(＋3))
＋(－3) ＝ (－3) ＝ －(＋3)
(＋1) × (－3) ＝ (－3) ＝ (－1) × (3)
(＋1) • (－3) ＝ (－3) ＝ (－1) • (＋3)
(1) • (－3) ＝ (－3) ＝ (－1) • (3)
[－1] • (1) • (3)
(－1) • (3)
－ [ (1) • (3) ]
－ [ (＋1) • (3) ] ＝ －[ (＋1) • (3) ]
(＋1) × (－3) ＝ －[ (＋1) • (3) ] ＝ － [ (＋1) • (3) ] ＝ － (＋3) ＝ ＋ (－3) ＝ (－3)
(－1) × (－3) ＝ －[ (－1) • (3) ] ＝ － [ (－1) • (3) ] ＝ － (－3) ＝ ＋ (＋3) ＝ (＋3)
(＋3) ＝ (＋3) ＝ (＋3)
＋ (＋3) ＝ (＋3) ＝ ＋ (＋3)
＋ (＋3) ＝ (＋3) ＝ － (－3)
＋ (＋(＋3)) ＝ (＋3) ＝ － (＋(－3))
＋ (＋(＋3)) ＝ (＋3) ＝ ＋ (－(－3))
(＋(＋3)) ＝ (＋3) ＝ (－(－3))
＋(＋3) ＝ (＋3) ＝ －(－3)
(＋1) • (＋3) ＝ (＋3) ＝ (－1) • (－3)
음의 수직선, 양의 수직선, 음양의 수직선, 수직선( 음양의 수직선에서 plus기호 생략)
https://www.zerodal.com/2023/11/111-1-3-3-3-3.html
https://www.zerodal.com/2023/11/112-2-3-6-6-6.html
https://www.zerodal.com/2023/11/113-6-2-3-3-3.html
https://www.zerodal.com/2023/11/114-by-common-sense.html
https://www.zerodal.com/2023/11/115-3-3-0-setoff.html
https://www.zerodal.com/2023/11/116-3-3.html
-----------------------------------------------------------------
https://www.zerodal.com/2023/11/001_17.html
(－3) ＝ (－3) ＝ (－3)
＋ (－3) ＝ (－3) ＝ ＋ (－3)
＋ (－3) ＝ (－3) ＝ － (＋3)
＋ (＋(－3)) ＝ (－3) ＝ － (＋(＋3)) * (－3)
＋ (＋(－3)) ＝ (－3) ＝ ＋ (－(＋3))
(＋(－3)) ＝ (－3) ＝ (－(＋3))
＋(－3) ＝ (－3) ＝ －(＋3)
(＋1) × (－3) ＝ (－3) ＝ (－1) × (3)
(＋1) • (－3) ＝ (－3) ＝ (－1) • (＋3)
(1) • (－3) ＝ (－3) ＝ (－1) • (3)
[－1] • (1) • (3)
(－1) • (3)
－ [ (1) • (3) ]
－ [ (＋1) • (3) ] ＝ －[ (＋1) • (3) ]
(＋1) × (－3) ＝ －[ (＋1) • (3) ] ＝ － [ (＋1) • (3) ] ＝ － (＋3) ＝ ＋ (－3) ＝ (－3)
(－1) × (－3) ＝ －[ (－1) • (3) ] ＝ － [ (－1) • (3) ] ＝ － (－3) ＝ ＋ (＋3) ＝ (＋3)
(＋3) ＝ (＋3) ＝ (＋3)
＋ (＋3) ＝ (＋3) ＝ ＋ (＋3)
＋ (＋3) ＝ (＋3) ＝ － (－3)
＋ (＋(＋3)) ＝ (＋3) ＝ － (＋(－3))
＋ (＋(＋3)) ＝ (＋3) ＝ ＋ (－(－3))
(＋(＋3)) ＝ (＋3) ＝ (－(－3))
＋(＋3) ＝ (＋3) ＝ －(－3)
(＋1) • (＋3) ＝ (＋3) ＝ (－1) • (－3)
음의 수직선, 양의 수직선, 음양의 수직선, 수직선( 음양의 수직선에서 plus기호 생략)
https://www.zerodal.com/2023/11/111-1-3-3-3-3.html
https://www.zerodal.com/2023/11/112-2-3-6-6-6.html
https://www.zerodal.com/2023/11/113-6-2-3-3-3.html
https://www.zerodal.com/2023/11/114-by-common-sense.html
https://www.zerodal.com/2023/11/115-3-3-0-setoff.html
https://www.zerodal.com/2023/11/116-3-3.html
-----------------------------------------------------------------
https://www.zerodal.com/2023/11/001_17.html
(참고사항)
중학생 때에, 단순히
음수와 양수의 곱셈과 나눗셈은, 같은 것끼리는 양수이고, 안 같은 것끼리는 음수.
음수와 양수의 덧셈과 뺄셈의 규칙은 ( - (-3) ) = ( + (+3) ), ( + (-3) ) = ( - (+3) )
외워서 쓴 기억 밖에는 없습니다.
이해의 어려움이 (허수 문턱)을 넘어 가는데 장애가 될 수 있습니다.
크게 보면
(허수의 문턱) ~> (복소평면 문턱) ~> (오일러 등식 문턱) ~> (복소 푸리에 적분 문턱)으로
상당히 문제가 많습니다. 인터넷 댓글에 보면,
좀 너무 심한 경우이기는 하지만 ( 음수 곱하기 음수는 양수... 더 보기
중학생 때에, 단순히
음수와 양수의 곱셈과 나눗셈은, 같은 것끼리는 양수이고, 안 같은 것끼리는 음수.
음수와 양수의 덧셈과 뺄셈의 규칙은 ( - (-3) ) = ( + (+3) ), ( + (-3) ) = ( - (+3) )
외워서 쓴 기억 밖에는 없습니다.
이해의 어려움이 (허수 문턱)을 넘어 가는데 장애가 될 수 있습니다.
크게 보면
(허수의 문턱) ~> (복소평면 문턱) ~> (오일러 등식 문턱) ~> (복소 푸리에 적분 문턱)으로
상당히 문제가 많습니다. 인터넷 댓글에 보면,
좀 너무 심한 경우이기는 하지만 ( 음수 곱하기 음수는 양수... 더 보기
(참고사항)
중학생 때에, 단순히
음수와 양수의 곱셈과 나눗셈은, 같은 것끼리는 양수이고, 안 같은 것끼리는 음수.
음수와 양수의 덧셈과 뺄셈의 규칙은 ( - (-3) ) = ( + (+3) ), ( + (-3) ) = ( - (+3) )
외워서 쓴 기억 밖에는 없습니다.
이해의 어려움이 (허수 문턱)을 넘어 가는데 장애가 될 수 있습니다.
크게 보면
(허수의 문턱) ~> (복소평면 문턱) ~> (오일러 등식 문턱) ~> (복소 푸리에 적분 문턱)으로
상당히 문제가 많습니다. 인터넷 댓글에 보면,
좀 너무 심한 경우이기는 하지만 ( 음수 곱하기 음수는 양수 )가 이해가 되질 않아서
수학공부 등한시 하는 경우도 있습니다.
시기적으로 중학교 입학할 학생이 있는 경우에,
겨울방학 중에 부모님이나 누님,형님과 같이 공부 해 두는 것도 좋아 보입니다.
-----------------------( * 수포자 = 수학공부 포기한 자 )------------------------
수학공부 과정에 학생들 발목을 잡고 늘어 지는 부분이, 더 정확하게 수포자로 만든 것이
( 음수 곱하기 음수는 양수 ) 및 ( 기초 미적분 공부 ), 이 두 가지입니다.
----------------------------------------------------------------------------------------------------
( 음수 곱하기 음수는 양수 ) 에서 데카르트좌표 유도가 되고
( 음수 )에서 ( 허수 )가 유도 되고
( 데카르트좌표 + 허수 + 음수 )에서 복소평면 유도가 되고
( 복소평면 + 허수 )에서 ( 오일러등식) 유도가 되고
더 나아가 (허수 + 기초 미적분)을 가지고 (복소 푸리에 적분)을 유도 합니다.
즉 실타래처럼 엮여 있습니다.
(복소 푸리에 적분) : 전기, 전자, 통신 쪽에는 매우 기초적인 내용입니다.
(기초 미적분)이 부실하면 ( 확률통계 ) 공부하는데도 문제가 많습니다.
상대(경제학과, 경영학과, ...) 쪽에서 꼭 배우는 수학은
(1) 벡터와 행렬 <~ (기초 미적분)이 필요
(2) 미적분 <~ (기초 미적분)이 필요
(3) 확률통계 <~ (기초 미적분)이 필요
(기초 미적분)은
연속(수의 연속)에서는 사실상 현실적으로 어렵고 어렵게 느껴질 수 있지만
이산(물질의 연속)에서는 ( 2 + 3 = 5 )라는 정도의 매우 단순한 계산도구입니다.
(기초 미적분)을 잘하기 위해서는
1. 직선의 방정식
2. 원의 방정식
3. 포물선방정식
4. 타원방정식
5. 쌍곡선방정식
6. 1,2,3,4차 함수
7. 삼각함수
8. 로그함수
9. 벡터함수
....
뒤에 방정식 및 함수가 붙어 있는 별로 재미없는 걸 공부해야 한다는 사실.....
위의 내용은 실용적인 수학에서 사용하기 때문에 반드시 필히 공부해야 하는 부담감 .....
공자 가라사대 : 삼인행에 유인사라.
Does a negative times a negative equal a positive, really?
( Equality and Double Balance Scale )
What is the difference between negative sign and minus sign?
What is the difference between positive sign and plus sign?
It is more important than ( A negative times a negative).
if, promise, [ Subtract sign(－), Add sign(＋) ]
[ Minus sign( ? ), Plus sign( ? ) ]
[ Negative sign( ? ), Positive sign( ? ) ]
Why? Subtract sign(－) ＝ Minus sign(－) ＝ Negative sign(－)
Why? Subtract sign(－) ＝ Minus sign(－) ＝ Debt sign(－)
Why? Subtract sign(－) ＝ Minus sign(－) ＝ Obligation sign(－)
Why? Add sign(＋) ＝ Plus sign(＋) ＝ Positive sign(＋)
Why? Add sign(＋) ＝ Plus sign(＋) ＝ Money sign(＋)
Why? Add sign(＋) ＝ Plus sign(＋) ＝ Claim sign(＋)
( 6 Minutes ) Does a negative times a negative equal a positive, really?
https://www.youtube.com/watch?v=YfbJlEbAjt4
( 8 Minutes ) Does a negative times a negative equal a positive, really?
https://www.youtube.com/watch?v=NtZsNm8WDek
Multiplication on Negative and Positive numbers
https://youtu.be/HitdYTgF6eQ?si=YjgwiqzbrfXkjntB
중학생 때에, 단순히
음수와 양수의 곱셈과 나눗셈은, 같은 것끼리는 양수이고, 안 같은 것끼리는 음수.
음수와 양수의 덧셈과 뺄셈의 규칙은 ( - (-3) ) = ( + (+3) ), ( + (-3) ) = ( - (+3) )
외워서 쓴 기억 밖에는 없습니다.
이해의 어려움이 (허수 문턱)을 넘어 가는데 장애가 될 수 있습니다.
크게 보면
(허수의 문턱) ~> (복소평면 문턱) ~> (오일러 등식 문턱) ~> (복소 푸리에 적분 문턱)으로
상당히 문제가 많습니다. 인터넷 댓글에 보면,
좀 너무 심한 경우이기는 하지만 ( 음수 곱하기 음수는 양수 )가 이해가 되질 않아서
수학공부 등한시 하는 경우도 있습니다.
시기적으로 중학교 입학할 학생이 있는 경우에,
겨울방학 중에 부모님이나 누님,형님과 같이 공부 해 두는 것도 좋아 보입니다.
-----------------------( * 수포자 = 수학공부 포기한 자 )------------------------
수학공부 과정에 학생들 발목을 잡고 늘어 지는 부분이, 더 정확하게 수포자로 만든 것이
( 음수 곱하기 음수는 양수 ) 및 ( 기초 미적분 공부 ), 이 두 가지입니다.
----------------------------------------------------------------------------------------------------
( 음수 곱하기 음수는 양수 ) 에서 데카르트좌표 유도가 되고
( 음수 )에서 ( 허수 )가 유도 되고
( 데카르트좌표 + 허수 + 음수 )에서 복소평면 유도가 되고
( 복소평면 + 허수 )에서 ( 오일러등식) 유도가 되고
더 나아가 (허수 + 기초 미적분)을 가지고 (복소 푸리에 적분)을 유도 합니다.
즉 실타래처럼 엮여 있습니다.
(복소 푸리에 적분) : 전기, 전자, 통신 쪽에는 매우 기초적인 내용입니다.
(기초 미적분)이 부실하면 ( 확률통계 ) 공부하는데도 문제가 많습니다.
상대(경제학과, 경영학과, ...) 쪽에서 꼭 배우는 수학은
(1) 벡터와 행렬 <~ (기초 미적분)이 필요
(2) 미적분 <~ (기초 미적분)이 필요
(3) 확률통계 <~ (기초 미적분)이 필요
(기초 미적분)은
연속(수의 연속)에서는 사실상 현실적으로 어렵고 어렵게 느껴질 수 있지만
이산(물질의 연속)에서는 ( 2 + 3 = 5 )라는 정도의 매우 단순한 계산도구입니다.
(기초 미적분)을 잘하기 위해서는
1. 직선의 방정식
2. 원의 방정식
3. 포물선방정식
4. 타원방정식
5. 쌍곡선방정식
6. 1,2,3,4차 함수
7. 삼각함수
8. 로그함수
9. 벡터함수
....
뒤에 방정식 및 함수가 붙어 있는 별로 재미없는 걸 공부해야 한다는 사실.....
위의 내용은 실용적인 수학에서 사용하기 때문에 반드시 필히 공부해야 하는 부담감 .....
공자 가라사대 : 삼인행에 유인사라.
Does a negative times a negative equal a positive, really?
( Equality and Double Balance Scale )
What is the difference between negative sign and minus sign?
What is the difference between positive sign and plus sign?
It is more important than ( A negative times a negative).
if, promise, [ Subtract sign(－), Add sign(＋) ]
[ Minus sign( ? ), Plus sign( ? ) ]
[ Negative sign( ? ), Positive sign( ? ) ]
Why? Subtract sign(－) ＝ Minus sign(－) ＝ Negative sign(－)
Why? Subtract sign(－) ＝ Minus sign(－) ＝ Debt sign(－)
Why? Subtract sign(－) ＝ Minus sign(－) ＝ Obligation sign(－)
Why? Add sign(＋) ＝ Plus sign(＋) ＝ Positive sign(＋)
Why? Add sign(＋) ＝ Plus sign(＋) ＝ Money sign(＋)
Why? Add sign(＋) ＝ Plus sign(＋) ＝ Claim sign(＋)
( 6 Minutes ) Does a negative times a negative equal a positive, really?
https://www.youtube.com/watch?v=YfbJlEbAjt4
( 6 Minutes ) Does a negative times a negative equal a positive, really?
( 8 Minutes ) Does a negative times a negative equal a positive, really?
https://www.youtube.com/watch?v=NtZsNm8WDek
( 8 Minutes ) Does a negative times a negative equal a positive, really?
Multiplication on Negative and Positive numbers
https://youtu.be/HitdYTgF6eQ?si=YjgwiqzbrfXkjntB
Multiplication on Negative and Positive numbers
| 목록 |
|
