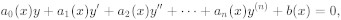- 회원들이 추천해주신 좋은 글들을 따로 모아놓는 공간입니다.
- 추천글은 매주 자문단의 투표로 선정됩니다.
| Date | 21/07/25 23:54:33수정됨 | ||
| Name | 매뉴물있뉴 | ||
| Subject | 예측모델의 난해함에 관하여, .feat 맨날 욕먹는 기상청 | ||
|
사실 기상청의 기상 예보가 어렵다는 사실은 잘 알려져 있습니다. 여러가지 직관적인 설명들이 있거든요. 베이징에서 나비가 날개를 펄럭이면 미국에 허리케인이 생긴다는 미중갈등... 아니 이게 아닌데?;; 암튼 '나비효과'라거나 '복잡계 이론'이라거나... 하는 등의 단어들 덕분이겠죠. (...근데 나비효과는 타임패러독스 영화 아니었나??) 다만, 기상 예측이 어렵다는 것이 알려져있다는 것과는 별개로, [기상 예측이 왜 어려운지를 이해]하는 것은 사실 NEXT LEVEL의 지식입니다. 그리고 이것을 이해하는데 필요한 예비지식의 많은 부분 중/고등학교 수학/ 고등학교 과학 레벨에 있기는 합니다만 대학 학부영역에도 다수 포함되어 있습니다. 그것도 물리학/ 수학/ 컴퓨터사이언스/ 지구과학 등등등 곳곳에 흩어져 있어요. 제가 오늘 활용할 영역의 지식은 대략 이렇습니다. 2차함수 (중학교 수학) 미분, 적분 (고등학교 수학) 미분방정식 (학부1,2학년 수학) 비선형방정식 모델링(학부3학년 정도?) 등은 대학 학부 영역에 있어요. 저는 이 글에서 나 문과나온 사람이야-ㅁ-!! 하시는 선생님들도 이해할수 있을법한 수준까지 기상예측의 난해함, 그중에서도 [컴퓨터 시뮬레이션의 난해함]에 대해 설명하고자 노력할것입니다. 그래서 저는 오늘 비선형방정식중 가장 간단한 방정식인 [y=x²]의 그래프를, 이 함수의 미분형태와 프로그램을 활용해서 그려볼것입니다. 처음에는 굉장히 부정확하게 그릴거에요. 그다음엔 정교하게 그릴겁니다. 그 다음엔 더 정교하게 그리고 더더더더더더더더 정교해지던 그래프가 어느 순간에는 다시 부정확해지는 것을 보여드릴 생각입니다. 지금쯤 이게 뭔소린가 잘 모르겠다. 정신이 아득해지는 느낌이 들고있다. 하신다면 선생님은 대단히 정상이십니다. 당황하지 마세요. 그래서 그림을 여럿 준비했습니다. 교과서는 그림이 많을수록 좋은 교과서니까요. 글은 사람을 산만하고 피곤하게 하지만 사진과 그림은 사람을 편안하고 안정감있게 합니다.  아아... 진욱이형 잘생겼다...... 이런 불공정한 세상 같으니...... 크릉 [미분] 이제 '미분'을 짚고 넘어갑시다. 그리고 사실 미분, 길게 설명 안할것입니다?? 선생님들이 지금보다도 더 똑똑하고 총명하셨을 고등학교때도 이해하기 어려우셨던것. 제가 이제 와서 글 두어줄 쓴다고... 갑자기 이해가 가는게 더 이상하니까요??  자자. 미분은 이렇게 동영상으로 보시듯 그래프의 '기울기'를 구하는 과정입니다? 물론 다들 이해하셨을테니, (찡긋) 넘어가겠읍니다. [미분방정식] 미분방정식이라고 하면 보통은, '방정식의 미분항이 제거되지 못하고 그대로 남아있는' 방정식를 말합니다. 다르게 표현하면, '방정식의 기울기'는 비교적 정확하게 알고있으나, '방정식 그 자체는 잘 모르는 경우'를 말합니다. 예를들어 y' = 2x 같은 방정식이라면?? y = x² + a의 형태로 적분을 통해 본래 방정식을 손쉽게 풀어낼수 있죠? 그래서 보통 저런건, 미분방정식이라고 취급해주지 않습니다. 누가 1+1=2 가 어려워서 수학을 포기하던가욥? 사소한 녀석 같으니...! 미분방정식은, 고등학교 과정에는 나오지 않지만 그렇다고 해서 미분방정식이 희귀하지는 않습니다. 사실은 굉장히 흔한 것입니다?? 이름만은 유명한 슈뢰딩거 방정식도, 미분방정식이고요, 선생님들이 혹시 수학을 조금이라도 다루는 학문을 전공과목으로 배우셨다면 그 학문의 어딘가에는 분명히 유명한 미분방정식이 한두개쯤은 존재할만큼?? 그 생각보다 흔합니다. 미분방정식 중 쉬운것을 고르자면... 아마도, '로트카-볼테라 방정식'이 가장 이해하기 쉬울텐데요,  사자에게 사슴이 잡아먹히면서, 숫자가 늘어나다 줄어들다 하는 것을 수식으로 표현한 것입니다. 사슴이 늘어나면 --> 사슴을 잡아먹는 사자의 숫자도 늘어납니다?? --> 하지만 사자가 늘어자면 사슴이 잡아먹히는 속도가 빨라지고 --> 사슴이 줄어들겠죠? --> 그럼 먹이가 부족해진 사자들은 다시 줄어들고?!?! --> 사자가 줄어들어서 사슴이 안잡아먹히고?!?! --> 사슴이 다시 늘어납니다??? 하는 무한루프를 말합니다. 이것을 수식으로 표현하면 이렇게 표현됩니다.  위의 방정식은 사슴의 증가율 아래 방정식은 사자의 증가율 인것?? 방정식은 뭔가 이해하기 어렵죠? 하지만 그림과 같이 보면 사실 어렵지 않아요.  (빨간게 사자, 녹색이 사슴) 사슴의 숫자가 증가하고 감소하는 그래프가 물결치는 그림이 사자의 숫자 그래프의 물결보다 묘하게 살짝 앞서 물결치는 그림이 나옵니다. [미분방정식을 컴퓨터로 푸는 방법] 하지만 제가 오늘 풀어드릴 방정식은 로트카-볼테라 방정식이 아닙니다. 그거보다 훨신 간단한것, 저는 오늘, y' = 2x 를 컴퓨터로 시뮬레이션하여 풀어드릴것이에요. 로트카-볼테라 방정식은 y = ******* x = ******* 의 형식으로 풀어낼수가 없습니다?? ---> 시뮬레이션을 해도, 그것을 검산할수는 없다는 겁니다?? 답을 모르니까요???? 오늘 저는 선생님들과 미분방정식인 y' = 2x만을 갖고서, y = x²를 풀어볼 것이에욤. 검산이 가능하니까욥?? 앞으로 갈길이 멉니다. 먼길 떠나기 전에, 윈터눈나 보고 가실께욥...  아아... 빠져든다... 마음이 안정되고 정화된다ㅏㅏㅏㅏㅏ....... [y'=2x를 그려보자] 저기요? 제가 뭐하는 중인지 기억 나시죱? ㅋㅋㅋㅋ 저는 y' = 2x의 그래프를 프로그램을 활용하여, 그릴것입니다. 왜 하필이면 y' = 2x 인가??? 두가지 이유가 있습니다. 1 일단은 비선형방정식중에 가장 쉬운 녀석이고요 2 검산이 가능하기 때문입니다. 로트카-볼테라 방정식은 시뮬레이션해서 풀더라도, 검산을 할수가 없습니다?? 하지만 y' = 2x 는 y = x²라는 답이 있어서, 검산을 할수 있을 것입니다?? 그래서 y' = 2x 를 그려볼 것 입니다??? 계산방법은 이렇습니다. 0) y' = 2x 를 갖고, (x, y) 그래프를 그릴 것입니다. 1) x, y = (0, 0)에서 출발합니다. 2) 0 < x < 4 구간만 그릴것입니다. 3) 프로그램이 무수히 많은 직선을 그려서 곡선을 따라가는 형태로 갈것 입니다. 무슨 말인지 잘 안와닿죠? 손으로 두번만 그려보겠습니다. [첫번째 그래프, 수동 4단계] 1) x=0일때, y'(직선의 기울기=2x)는 0입니다. 기울기가 0인 직선을 (0, 0)에서 (1, 0)까지 그립니다. 2) x=1일때, y'(직선의 기울기=2x)는 2입니다. 기울기가 0인 직선을 (1, 0)에서 (2, 2)까지 그립니다. 3) x=2일때, y'(직선의 기울기=2x)는 4입니다. 기울기가 0인 직선을 (2, 2)에서 (3, 6)까지 그립니다. 4) x=3일때, y'(직선의 기울기=2x)는 6입니다. 기울기가 0인 직선을 (3, 6)에서 (4, 12)까지 그립니다. 이것을 그래픽으로 표현하면 다음과 같습니다.  [두번째 그래프, 수동 8단계] 1) x=0일때, y'(직선의 기울기=2x)는 0입니다. 기울기가 0인 직선을 (0, 0)에서 (0.5, 0)까지 그립니다. 2) x=0.5일때, y'(직선의 기울기=2x)는 1입니다. 기울기가 1인 직선을 (0.5, 0)에서 (1, 0.5)까지 그립니다. 3) x=1일때, y'(직선의 기울기=2x)는 2입니다. 기울기가 2인 직선을 (1, 0.5)에서 (1.5, 1.5)까지 그립니다. 4) x=1.5일때, y'(직선의 기울기=2x)는 3입니다. 기울기가 3인 직선을 (1.5, 1.5)에서 (2, 3)까지 그립니다. 5) x=2일때, y'(직선의 기울기=2x)는 4입니다. 기울기가 4인 직선을 (2, 3)에서 (2.5, 5)까지 그립니다. 6) x=2.5일때, y'(직선의 기울기=2x)는 5입니다. 기울기가 5인 직선을 (2.5, 5)에서 (3, 7.5)까지 그립니다. 7) x=3일때, y'(직선의 기울기=2x)는 6입니다. 기울기가 6인 직선을 (3, 7.5)에서 (3.5, 10.5)까지 그립니다. 8) x=3.5일때, y'(직선의 기울기=2x)는 7입니다. 기울기가 7인 직선을 (3.5, 10.5)에서 (4, 14)까지 그립니다.  기왕만들었으니, 옆에 놓고 같이 볼까요?
왼쪽의 그림은 4단계 오른쪽의 그림은 8단계 입니다. 4단계시뮬레이션에서, y의 추정값은 12 8단계시뮬레이션에서, y의 추정값은 14, 입니다. y의 실제값은 16이니까, 단계가 늘어나니 뭔가 좀 정확해졌죠? [자동으로 그래프 그리기] 4단계, 8단계 다음은 40단계, 400단계, 4000단계, 40000단계 하는식으로 쭉쭉쭉쭉 가서 4백만단계, 8백만단계 까지 간 뒤에 멈출 것입니다. 왜 멈추는지는 이따가 설명 드릴게요. 아래는 만들어진 그래프들의 모양들입니다. -엑셀로 그려서 가독성이 조금 거시기할수 있읍니다-   파란색이 시뮬레이션 결과이고 노란색이 실제 정답입니다. 시뮬레이션을 더 정밀하게 할수록 정답에 가까워 지는 것을 볼수 있습니다. 하지만 정밀하면 더 정밀해질수록 정답에서 멀어지는 현상도 보이네요?? 그러면 이제는 이 '오차'에만 집중해서 보시겠습니다.  의외죠?? 4000단계로 나누어서 계산했을때가 가장 정확한 값을 구할수 있었읍니다?? 4000단계보다 4만회가 더 부정확하고 40만회는 더 부정확해졌는데 더더더더 정밀하게 계산해보자고 400만, 800만단계로도 나누어 계산했더니??? 더욱더 부정확해졌어욥?? 이유는 여러가지가 있읍니다만, 그 이유중 하나는 float이라고 하는, 컴퓨터가 '실수(Real Number)'를 표현하는 방법, 때문입니다. [float은 무엇이란 말인가] float은 숫자를 저장하는 형식중 하나입니다. float형식은 유효숫자의 자리수에 한계가 있기 때문에 만약 제가 123456789라는 숫자를 float으로 저장하려고하면 1.23456789 * 10^8로 변환한뒤 1.2345679 * 10^8의 형태로 반올림해버린 뒤에 숫자를 저장합니다. 맨끝의 9가 반올림 되어버렸기 때문에, float으로 저장된 숫자를 나중에 복원해보면, 123456789가 아닌 123456790이 등장합니다. 이 버려지는 반올림이 너무 크게 누적되면, 결국에는 "정밀하게 계산하려고 하면 할수록" 부정확해지는 결과를 초래하게 되는거죠. 물론 이쯤 되면 많은 분들이 이미 정신이 아득해져서 '이게 지금 무슨 소리인가'하실겁니다. 나는 누군가, 여기는 어딘가 내가 지금 무슨 부귀영화를 누리겠다고 이런 뻘글을 읽는가 이해합니다. 제 필력이 뭐 그렇죠; ㅡ.ㅡ;;  짤 마려우신 것... 압니다. 하지만 지금 이 시점에서 아직 집중력을 잃지 않은분들이 계시다면, 아마도, 프로그래머 분들이 아니실까 합니다?? 프로그래머 분들은 아마 이렇게 생각하고 계실꺼에요. "그럼 float 대신 double을 쓰면 되지 않느냐?"라고 말이죱. 맞습니다? double을 쓰면 되겠죱?? 하지만 double을 쓴다고 해서 모든 문제가 다 해결되지는 않습니다. double을 쓰면 물론 더 정확해지겠죠. float은 소수점 아래 6자리 까지만 저장하지만 double은 소수점아래 10자리?? 까지 저장하니까요?? 하지만 double로도 해결할수 없는 문제는 아직 남아있습니다. 왜냐하면 우리는 지금, 중요한 전제 하나를 잊어버렸기 때문입니다. ['애초에 이렇게 프로그램을 돌려서 f(x)의 그래프를 그리는 기술이 필요한 이유']가 뭐였는지 기억하십니까? [f(x)의 방정식이 없을때 쓰려고] 그런겁니다. f'(x)의 방정식은 있는데!! f(x)의 방정식은 없을때!ㅠ 그럴때 쓰기 위해서 였던거죱? 다시 말하자면, 애초에 f(4)가 16인지 모를때만, 시뮬레이션을 돌린다는 말입니다. 자 그러면 이런 질문이 남습니다. "우리는 어떻게 시뮬레이션의 결과를 검증할수 있는걸까요??"  위의 표는 float이 아닌, double로 만든 표입니다. 아까보다 뭔가 자리수가 더 정확해졌죠? 하지만 첫번째 표에 있는 것처럼 소수점 아래 7자리까지를 다 신용할수 있을까요? 아뇨, 사실은 그럴수가 없습니다. 그러면, 4E+9, 4E+10, 4E+11 세개의 결과가 서로 일치하는듯...하니까? 정답은 15.999999라고 결론내릴수 있을까요? 아뇨, 그럴수 없습니다. 그리고 사실 그렇게 하면, 오답이되죠; 15.999999의 오차범위는 플러스마이너스 0.0000005니까요. 이 표를 보고 정답을 고르려면, 4E+4부터 4E+11이 지지하는 16.000까지를 정답으로 취하고 나머지 소수점 네자리는 버려야 정답이 됩니다. 열세번의 계산 끝에, 소수점 7자리까지 정확하게 계산해낸 한번의 계산이 있었다고 해서 그 7자리를 정확하게 취할수 있을까요??? 실제로는 그렇게 할수 없고, 소수점아래 세자리만 까지만 반올림해서 취하고, 나머지 4자리는 버려야만 합니다. 어쩌다보니 소수점아래 7자리까지 정확하게 계산해낸 시뮬레이션이 존재한다고 해서 그 시뮬레이션이 정답이고, 다른 시뮬레이션이 틀렸다는 것을 증명할 방법은?? 사실 없으니까요. 시뮬레이션이 정확한들, 답을 미리 알고 있지 않았다면 무슨 의미일까요. 따라서 시뮬레이션의 끝에는, 반드시 사람의 해석이 존재하게 됩니다. float을 사용해서 계산했다면 f(4) = 1.6 * 10 double을 사용해서 계산했다면 f(4) = 1.6000 * 10 이다. 라는 결론이야 나올수 있읍니다만 [이것은 사실 '사람의 해석'..] 컴퓨터의 계산결과는 이것입니다?? 하고 뚝 던져줄수있는 방법은 사실상 없읍니다. 모든 시뮬레이션의 끝에는, 이런 사람의 해석이 들어갈수밖에 없는것이죠. [기상청의 예보는 이보다 더 어려운 이유] 우리가 오늘 살펴본 함수는 이차함수로써 사실 비선형 그래프들중에 제일 쉬운 놈입니다. 기상청에서 다루는 그래프들은 그런데 다들 이보다 난해한 그래프들 뿐이에요. 뉴턴의 냉각법칙은 지수함수로 되어있습니다. 바다에서 시간당 증발량을 구하려면? 태양이 내리쬐는것도 감안해야하지만 습도가 변하면 기체분압이 변하는 것도 고려해야 합니다?? 게다가 이 기체분압 공식은 뭐라고 표현해야할지도 모르겟읍니다...... 거지같이 생긴 분수공식-ㅁ-??? 기압/온도에 따라 이슬점이 변하는건... 뭐라고 표현하지...?? 난수표???;; 그 진짜 하나같이 난해한 것 투성이에요. 저희들이 오늘 y=x²를 그려볼때는, 수식이 있으니 검증이라도 할수있었지만, 기상청이 본인들의 기상예측을 검증하는 방법은 우리에게도, 그들에게도 딱 하나뿐. 실제 그 날짜가 되어, 비가 오는지 안오는지 관측하는 것 뿐입니다. 하지만 지구 온난화가 계속되면서 지구전체의 평균기온은 상승했고, 기상청은 이제 새로운 도전에 직면해 있습니다. 평균기온이 상승하기 전에 사용하던 모델들이 모두다 어딘가 어긋나고 부정확해진 것이죠. 평균기온이 상승해버린 지구는 평균기온이 상승하기 전과는 다른 온도에서, 다른 습도에서 다른 날씨를 보여주니까요. 기상 예측 기술이 발달해온 속도보다도 기상 예측 난이도가 상승하는 속도가 훨씬 빨라져버린겁니다. [기상청이 욕을 먹는 또 다른 이유] 생각해보시면, 대부분의 다른 과학/기술분야들은 보통 그 기술이 엄청 발달을 해서 정확도/정밀도가 엄청 올라가고 그로인한 부가가치 창출이 어마어마해져야 사실 주목을 받습니다. 반도체, 스마트폰, 인터넷, 자동차 등등, 다 똑같은 경우죠. 반면 기상청이 주목을 받는 이유는, 주식이 주목받는 이유와 비슷합니다. '날씨는 돈이 되기 때문'이죠. 가을 김장 배추 파종기에는 항상 태풍이 옵니다. 때문에 태풍이 제주, 경상, 전라, 충청, 경기, 중에 어느 쪽을 강하게 때리고 지나가느냐에 따라 김장철 배추의 시세가 엄청나게 폭등하고, 또 폭락합니다. 비가 연이어 이어지는 바람에 건설현장의 공기가 하루 이틀 연장되면서 수억이 왔다갔다하는 경우도 흔하고 올 여름이 더울꺼라고 예측한 에어컨 공장들이 봄에 공장을 돌려 미리 재고를 넉넉하게 쌓아두었다가, 여름이 생각보다 덥지 않기라도 하면 에어컨 공장들은 그대로 재고를 떠안거나 눈물의 세일을 해서 팔아치우는 것을 우리는 종종 목격하니까요. 때문에, 기상예측은 분명 과학분야임에도 불구하고 다른 과학분야와는 조금 다른 대우를 받는 경향이 있읍니다. 정밀도/정확도가 충분하지 않아서 관심을 많이 받을 준비가 덜 되어 있는데도 이미 관심이 너무 많은 관심이 쏟아지고 있는 경우인 것. 이런저런 이유로 날씨예보가 틀릴 경우에 기상청에 쏟아지는 비난은 [이 사기꾼들], [구라청] 같은 멸칭들. 그... 가만 생각해보시면 보통 저런 명칭은 과학자들에게 붙는 비난이라기 보다는 오히려 주식리딩방의 예측이 틀렸을 경우에 붙는 종류들 같지 않으시던가요?? 그런데 저런 주식리딩방 방장들은 기상청과는 다르게 그.... 말빨이........ 좋읍니다 (굳) 아무리 자기가 사기를 치고난 직후라도 말빨을 이리저리 굴리고, 요리저리 피해가기라도 잘 피해가는데 우리의 기상학자들은 뭔가... 그... 뭐랄까... ......체크무늬 남방을 참 좋아하시는것 같읍니다 허허;;;;;; 근데 가만보면 이 사람들이, 또 그런 사람들만 모여 있어요. 1 관측도 해야하고, 2 물리도 해야하고 3 컴퓨터도 수준급으로 다뤄야 할뿐 아니라 4 화학도 다루고, 5 지구과학도 다뤄야 하고 심지어는 6 인공위성과 7 무선통신, 8 실외계측까지도 다룹니다?? 은근, 이공계의 온갖 너드들이 다 모여야 돌아가는 분야가 기상 예측 분야인데다가 실제로 기상예측쪽에 종사하시는 분들을 가끔 뵐때면 뭔가 항상 죄송하고 미안해하는... 마인드로 무장하고 계셔서 안쓰러운데 말빨마져도(..........) 안습하신것; 괜히 기상캐스터라는 직군이 따로 만들어진게 아니구나... 라는 생각, 매번 하고있읍니다. ㅇㄱㄹㅇ 이 분야가, 그 상상 이상으로 해석의 오랜 노하우가 축적된 고인물들이 많이 필요한 분야인데 막상 전문가들은 소심하고 외톨이같은 INTP들만 그득하고 전국민들에게 댓글로 욕먹다말고 몇년 일하다 마음에 상처받고 이직해버리는 일이 잦읍니다. 기상해석을 생산해내는 분들과, 일반 대중간의 간극도 어느정도는 좁아질 필요가 있지 않나 싶어서 주말내내 무리해서 타이핑을 하는 중입니다. 으윽 이과력이 부족하신 분들은 읽다 이해를 포기해서 여기까지 못읽으셨을것 같고 문과력이 부족하신 분들은 글이 길어서(.....) 읽다 포기하셨을것 같읍니다만 흑흑 저기요! 여기 세줄요약 있어요! 1 기상예측에 동원되는 방정식은 어딜봐도 비선형방정식 투성이. 2 미분방정식의 프로그램 시뮬레이션은 그 정확성을 담보하는데 한계가 있다. 3 기상예측은 결국에는 사람의 해석과 통밥이 필수적이라, 실수가 많아도 이해해줍시다. 4 이게 다 지구온난화 때문이다. 암튼 온난화 때문임. 요약이 네줄인건 기분탓. 좋은 밤 되세요. * Cascade님에 의해서 티타임 게시판으로부터 게시물 복사되었습니다 (2021-08-10 07:37) * 관리사유 : 추천게시판으로 복사합니다. 42
|
|||