- 질문 게시판입니다.
| Date | 25/05/19 17:36:50 |
| Name | 아침커피 |
| Subject | 무한 제곱근 속에 있는 변수의 값을 구할 때의 판별식(?) |
|
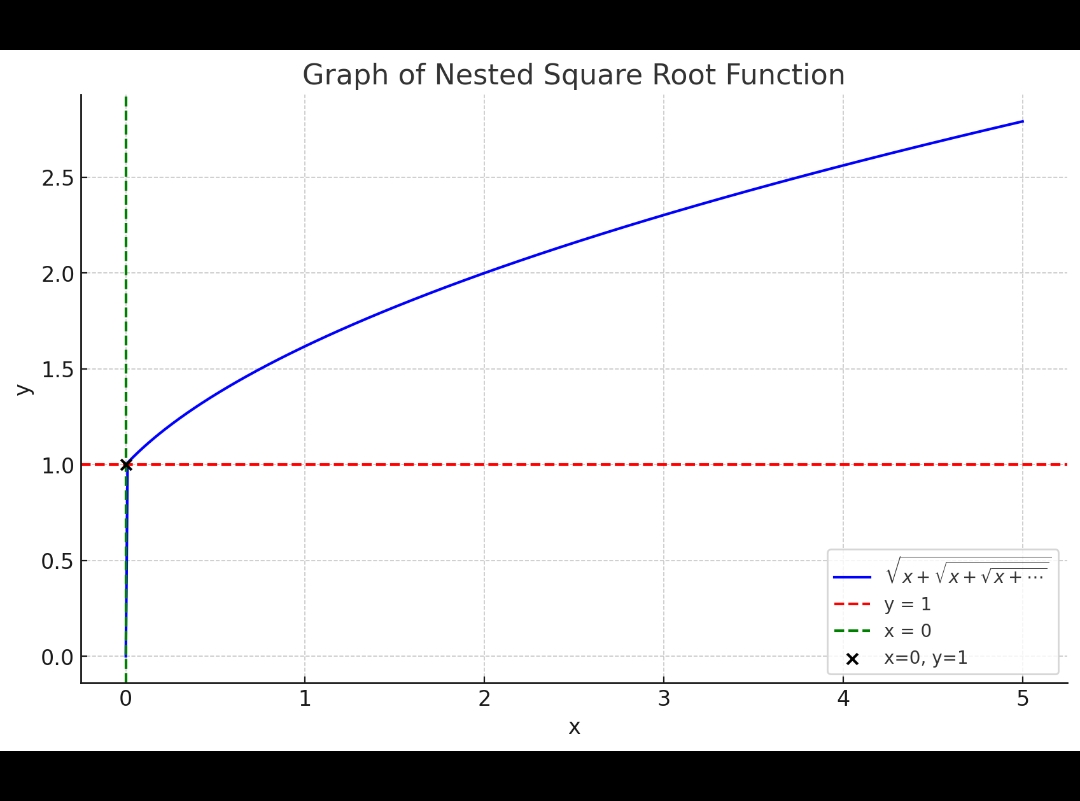
제곱근을 편의상 sqrt() 라고 쓰겠습니다. 예를 들어 이렇게 제곱근 속에 제곱근이 무한히 있을 경우 한번 제곱해준 다음에 다음과 같이 풀어주면 된다는 것을 알겠습니다. (1) 시작: sqrt(x + sqrt(x + sqrt(x + ...))) = 3 (2) 양쪽을 제곱해주면: x + sqrt(x + sqrt(x + sqrt(x + ...))) = 9 (3) 그런데 sqrt(x + sqrt(x + sqrt(x + ...))) = 3 이니까 x + 3 = 9 (4) 따라서 x = 6 이건 알겠는데요, 이렇게 풀 수 있는 제한조건이 있을 것 같은데 그게 뭔지를 모르겠습니다. 예를 들어서 위의 맨 처음 식에서 오른쪽의 3만 1로 바꿔보았는데 그랬더니 이상한 결과가 나옵니다. (1) 시작: sqrt(x + sqrt(x + sqrt(x + ...))) = 1 (2) 양쪽을 제곱해주면: x + sqrt(x + sqrt(x + sqrt(x + ...))) = 1 (3) 그런데 sqrt(x + sqrt(x + sqrt(x + ...))) = 1 이니까 x + 1 = 1 (4) 따라서 x = 0 ??? x = 0 이면 sqrt(x + sqrt(x + sqrt(x + ...))) 는 당연히 0일텐데??? 그래서... 질문을 요약하면 다음과 같습니다. (1) 뭔가 이런 방법으로 답을 구할 수 있는 경우가 한정되어있을 것 같은데, 그 조건이 어떻게 될까요? 질문을 쓰다 보니 지금 순간 든 생각이, 아마 x > sqrt(x) 라는 조건이 충족될 때에만 저런 식으로 답을 구할 수 있을 것 같은데 맞는지 모르겠네요. (2) sqrt(x + sqrt(x + sqrt(x + ...))) = 3 에서 x = 6이라고 구한 답은 맞는 답이기는 한가요? =_= 답변에 미리 감사드립니다. 0
이 게시판에 등록된 아침커피님의 최근 게시물
|
|
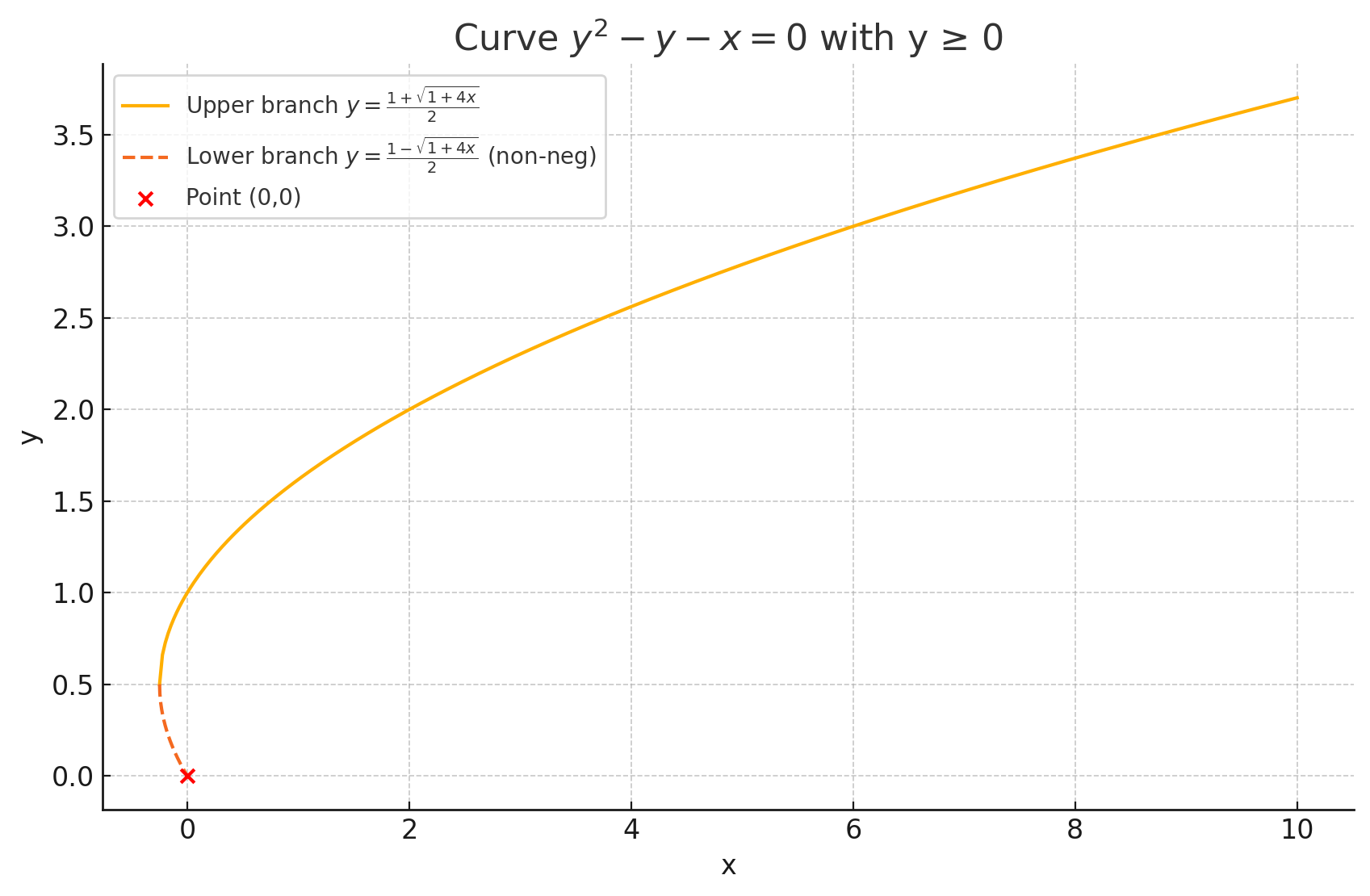
구하신 답은 맞구요. 제한조건은 x >= -1/4 이기만 하면 됩니다.
(4)에서 말씀하신 [x = 0 이면 sqrt(x + sqrt(x + sqrt(x + ...))) 는 당연히 0일텐데???]의 직관이 (표준해석학 입장에서는) 틀렸습니다.
sqrt(x + sqrt(x + sqrt(x + ...))) = y 로 두면,
y^2 - y + x = 0이고 y입장에서 이차방정식의 근의 공식을 적용하면
y = (1 + sqrt(1 + 4x))/2 이므로
표준해석학 입장... 더 보기
(4)에서 말씀하신 [x = 0 이면 sqrt(x + sqrt(x + sqrt(x + ...))) 는 당연히 0일텐데???]의 직관이 (표준해석학 입장에서는) 틀렸습니다.
sqrt(x + sqrt(x + sqrt(x + ...))) = y 로 두면,
y^2 - y + x = 0이고 y입장에서 이차방정식의 근의 공식을 적용하면
y = (1 + sqrt(1 + 4x))/2 이므로
표준해석학 입장... 더 보기
구하신 답은 맞구요. 제한조건은 x >= -1/4 이기만 하면 됩니다.
(4)에서 말씀하신 [x = 0 이면 sqrt(x + sqrt(x + sqrt(x + ...))) 는 당연히 0일텐데???]의 직관이 (표준해석학 입장에서는) 틀렸습니다.
sqrt(x + sqrt(x + sqrt(x + ...))) = y 로 두면,
y^2 - y + x = 0이고 y입장에서 이차방정식의 근의 공식을 적용하면
y = (1 + sqrt(1 + 4x))/2 이므로
표준해석학 입장에서 sqrt(x + sqrt(x + sqrt(x + ...))) = 1일 때 x = 0으로 [지정]하는 것이 자연스럽습니다.
(생각해보니 analytic continuation까지 갈 필요도 없군요 ㅎㅎ)
(4)에서 말씀하신 [x = 0 이면 sqrt(x + sqrt(x + sqrt(x + ...))) 는 당연히 0일텐데???]의 직관이 (표준해석학 입장에서는) 틀렸습니다.
sqrt(x + sqrt(x + sqrt(x + ...))) = y 로 두면,
y^2 - y + x = 0이고 y입장에서 이차방정식의 근의 공식을 적용하면
y = (1 + sqrt(1 + 4x))/2 이므로
표준해석학 입장에서 sqrt(x + sqrt(x + sqrt(x + ...))) = 1일 때 x = 0으로 [지정]하는 것이 자연스럽습니다.
(생각해보니 analytic continuation까지 갈 필요도 없군요 ㅎㅎ)
오 감사합니다! 이차방정식 형태로 바꿔서 푸는 방법이 있군요! 수학이 항상 그렇듯 궁금증 하나가 해결되니 다른 궁금증이 더 생기는데요 ㅋㅋㅋ
(1) x >= -1/4 라는 조건은 어떻게 해서 생겨나는 것인가요? -> 음 이건 글을 쓰다 보니 위 판별식에서 루트 안의 값이 음수가 되지 않는 조건이군요 ㅎㅎ
(2) 그리고 표준해석학에서는 sqrt(x + sqrt(x + sqrt(x + ...))) = 1일 때 x = 0으로 지정하는 것이 자연스럽다고 하셨는데, 이 경우에 대해 수학의 다른 분야에서는 이 x의 값을 다른 값으로 정하는 경우도 있는지,
(3) 마지막으로 수학 전공하시는 분들 중에서도 저처럼 '아니 왜 sqrt(0 + sqrt(0 + sqrt(0 + ...))) 이 0이 아니고 1이지 ㅠㅠ' 하며 이것이 직관적이지 않다고 생각하는 경우도 있는지 궁금합니다.
(1) x >= -1/4 라는 조건은 어떻게 해서 생겨나는 것인가요? -> 음 이건 글을 쓰다 보니 위 판별식에서 루트 안의 값이 음수가 되지 않는 조건이군요 ㅎㅎ
(2) 그리고 표준해석학에서는 sqrt(x + sqrt(x + sqrt(x + ...))) = 1일 때 x = 0으로 지정하는 것이 자연스럽다고 하셨는데, 이 경우에 대해 수학의 다른 분야에서는 이 x의 값을 다른 값으로 정하는 경우도 있는지,
(3) 마지막으로 수학 전공하시는 분들 중에서도 저처럼 '아니 왜 sqrt(0 + sqrt(0 + sqrt(0 + ...))) 이 0이 아니고 1이지 ㅠㅠ' 하며 이것이 직관적이지 않다고 생각하는 경우도 있는지 궁금합니다.
간단한 예를 하나 들어보겠습니다.
y = (x^2 - 1)/(x - 1) 이라는 함수가 있습니다.
이 함수는 x = 1에서는 정의되지 않지요. 왜냐하면 분모를 0으로 만드니까요.
그리고 x가 1이 아닐 때는 y = x + 1과 정확하게 같은 함수입니다.
자 그렇다면 함수 y = (x^2 - 1)/(x - 1) 에다가 x = 1에서의 함숫값을 굳이 [지정]해주고 싶다면 무엇으로 하는 것이 [자연]스러울까요?
생각하시는 [2]가 답이 맞습니다. 왜냐하면 2가 이 ... 더 보기
y = (x^2 - 1)/(x - 1) 이라는 함수가 있습니다.
이 함수는 x = 1에서는 정의되지 않지요. 왜냐하면 분모를 0으로 만드니까요.
그리고 x가 1이 아닐 때는 y = x + 1과 정확하게 같은 함수입니다.
자 그렇다면 함수 y = (x^2 - 1)/(x - 1) 에다가 x = 1에서의 함숫값을 굳이 [지정]해주고 싶다면 무엇으로 하는 것이 [자연]스러울까요?
생각하시는 [2]가 답이 맞습니다. 왜냐하면 2가 이 ... 더 보기
간단한 예를 하나 들어보겠습니다.
y = (x^2 - 1)/(x - 1) 이라는 함수가 있습니다.
이 함수는 x = 1에서는 정의되지 않지요. 왜냐하면 분모를 0으로 만드니까요.
그리고 x가 1이 아닐 때는 y = x + 1과 정확하게 같은 함수입니다.
자 그렇다면 함수 y = (x^2 - 1)/(x - 1) 에다가 x = 1에서의 함숫값을 굳이 [지정]해주고 싶다면 무엇으로 하는 것이 [자연]스러울까요?
생각하시는 [2]가 답이 맞습니다. 왜냐하면 2가 이 함수를 [연속함수]가 되게 해주니까요.
물론 2 말고 다른 값으로 지정해도 아무런 문제가 없습니다. 단지 그렇게 하면 연속함수가 되지 않지요.
(이건 어려운 얘긴데 2로 지정하지 않아도 y = (x^2 - 1)/(x - 1) 과 y = x + 1는 [almost everywhere] 같은 함수입니다. 참고: https://en.wikipedia.org/wiki/Almost_everywhere)
여기서 자연스럽다는 것은 그렇게 해야 연속함수로서 의미가 있다는 뜻입니다. ㅎㅎ
다른 분야를 떠나서 연속함수를 다루는 것이 쉬우니까 그렇게 지정하는 것이라 보시면 됩니다. :)
y = (x^2 - 1)/(x - 1) 이라는 함수가 있습니다.
이 함수는 x = 1에서는 정의되지 않지요. 왜냐하면 분모를 0으로 만드니까요.
그리고 x가 1이 아닐 때는 y = x + 1과 정확하게 같은 함수입니다.
자 그렇다면 함수 y = (x^2 - 1)/(x - 1) 에다가 x = 1에서의 함숫값을 굳이 [지정]해주고 싶다면 무엇으로 하는 것이 [자연]스러울까요?
생각하시는 [2]가 답이 맞습니다. 왜냐하면 2가 이 함수를 [연속함수]가 되게 해주니까요.
물론 2 말고 다른 값으로 지정해도 아무런 문제가 없습니다. 단지 그렇게 하면 연속함수가 되지 않지요.
(이건 어려운 얘긴데 2로 지정하지 않아도 y = (x^2 - 1)/(x - 1) 과 y = x + 1는 [almost everywhere] 같은 함수입니다. 참고: https://en.wikipedia.org/wiki/Almost_everywhere)
여기서 자연스럽다는 것은 그렇게 해야 연속함수로서 의미가 있다는 뜻입니다. ㅎㅎ
다른 분야를 떠나서 연속함수를 다루는 것이 쉬우니까 그렇게 지정하는 것이라 보시면 됩니다. :)
아, 제가 이해한 것이 맞네요 ㅎㅎ
일대일이어야 하니 x 하나, y 하나가 정해져야 하죠.
x = 0일 때 y를 1로 택하지 않고 0을 택한다면 불연속이 되죠.
다른 x들에서의 함수가 y = (1 [+] sqrt(1 + 4x))/2인데
x = 0에서만 y = (1 [-] sqrt(1 + 4x))/2를 택한다는 것은 부자연스럽다는 말입니다. :)
일대일이어야 하니 x 하나, y 하나가 정해져야 하죠.
x = 0일 때 y를 1로 택하지 않고 0을 택한다면 불연속이 되죠.
다른 x들에서의 함수가 y = (1 [+] sqrt(1 + 4x))/2인데
x = 0에서만 y = (1 [-] sqrt(1 + 4x))/2를 택한다는 것은 부자연스럽다는 말입니다. :)
자세히 설명해주신 것에 다시한번 감사드립니다. 좀 지난 질문입니다만 궁금한 게 생겨서 추가로 댓글을 달게 되었습니다. 다음과 같은 수열을 생각해 보았는데요.
a_0 = sqrt(0),
a_1 = sqrt(0 + sqrt(a_0))
a_k = sqrt(0 + sqrt(a_(k-1)))
이러면 lim(k->inf) a_k 가 본문의 sqrt(0 + sqrt(0+ sqrt(0 + ...)))이 되는데요, 수학적 귀납법을 쓰면 모든 k에 대해서 a_k가 0임이 증명이 되더라고요.
그래서, 위 식이 x가 0인 점에서는 불연... 더 보기
a_0 = sqrt(0),
a_1 = sqrt(0 + sqrt(a_0))
a_k = sqrt(0 + sqrt(a_(k-1)))
이러면 lim(k->inf) a_k 가 본문의 sqrt(0 + sqrt(0+ sqrt(0 + ...)))이 되는데요, 수학적 귀납법을 쓰면 모든 k에 대해서 a_k가 0임이 증명이 되더라고요.
그래서, 위 식이 x가 0인 점에서는 불연... 더 보기
자세히 설명해주신 것에 다시한번 감사드립니다. 좀 지난 질문입니다만 궁금한 게 생겨서 추가로 댓글을 달게 되었습니다. 다음과 같은 수열을 생각해 보았는데요.
a_0 = sqrt(0),
a_1 = sqrt(0 + sqrt(a_0))
a_k = sqrt(0 + sqrt(a_(k-1)))
이러면 lim(k->inf) a_k 가 본문의 sqrt(0 + sqrt(0+ sqrt(0 + ...)))이 되는데요, 수학적 귀납법을 쓰면 모든 k에 대해서 a_k가 0임이 증명이 되더라고요.
그래서, 위 식이 x가 0인 점에서는 불연속인 것이 아닌가 하는 생각이 들었습니다. 저는 해석학은 모르지만 수학적 귀납법을 써 보면 0이 답인 것 같아서요... 혹시 x=0일 때는 본문의 식이 불연속이고 답이 0일 수 있을까요? 만약 아니라면 (즉 답이 1이라면) 수학적 귀납법의 결과를 배제해야 하는 이유가 무엇이 될지도 궁금합니다.
a_0 = sqrt(0),
a_1 = sqrt(0 + sqrt(a_0))
a_k = sqrt(0 + sqrt(a_(k-1)))
이러면 lim(k->inf) a_k 가 본문의 sqrt(0 + sqrt(0+ sqrt(0 + ...)))이 되는데요, 수학적 귀납법을 쓰면 모든 k에 대해서 a_k가 0임이 증명이 되더라고요.
그래서, 위 식이 x가 0인 점에서는 불연속인 것이 아닌가 하는 생각이 들었습니다. 저는 해석학은 모르지만 수학적 귀납법을 써 보면 0이 답인 것 같아서요... 혹시 x=0일 때는 본문의 식이 불연속이고 답이 0일 수 있을까요? 만약 아니라면 (즉 답이 1이라면) 수학적 귀납법의 결과를 배제해야 하는 이유가 무엇이 될지도 궁금합니다.
일단 의도하신 점화식의 표현이 a_k = sqrt(0 + sqrt(a_(k-1))) 이 아니라 [a_k = sqrt(0 + a_(k-1))] 인 것 같네요 ㅎㅎ
제가 위에서 답변을 잘못한 것이 있긴 하군요. ㅎㅎ
선생님 말씀대로 초항인 a_0를 0으로 셋팅하면 0이 되는게 맞습니다.
하지만 분문의 선생님의 질문은 초기 항을 셋팅한 것이 아니라 결과를 먼저 생각한 것이죠. [sqrt(x + sqrt(x + sqrt(x + ...))) = 1]
sqrt(x + sqrt(x + sqrt(x + ...))) =... 더 보기
제가 위에서 답변을 잘못한 것이 있긴 하군요. ㅎㅎ
선생님 말씀대로 초항인 a_0를 0으로 셋팅하면 0이 되는게 맞습니다.
하지만 분문의 선생님의 질문은 초기 항을 셋팅한 것이 아니라 결과를 먼저 생각한 것이죠. [sqrt(x + sqrt(x + sqrt(x + ...))) = 1]
sqrt(x + sqrt(x + sqrt(x + ...))) =... 더 보기
일단 의도하신 점화식의 표현이 a_k = sqrt(0 + sqrt(a_(k-1))) 이 아니라 [a_k = sqrt(0 + a_(k-1))] 인 것 같네요 ㅎㅎ
제가 위에서 답변을 잘못한 것이 있긴 하군요. ㅎㅎ
선생님 말씀대로 초항인 a_0를 0으로 셋팅하면 0이 되는게 맞습니다.
하지만 분문의 선생님의 질문은 초기 항을 셋팅한 것이 아니라 결과를 먼저 생각한 것이죠. [sqrt(x + sqrt(x + sqrt(x + ...))) = 1]
sqrt(x + sqrt(x + sqrt(x + ...))) = 1 식에서 어울리는 x가 무엇이냐에 대한 질문을 하신 겁니다.
점화식 [a_k = sqrt(0 + a_(k-1))] 에서 k를 무한대로 보내면 X = sqrt(0 + X)의 해가 무엇이냐의 질문이 되죠. 아시다시피 X는 0 또는 1 입니다.
본문의 sqrt(x + sqrt(x + sqrt(x + ...))) = 3 에서 x = 6 으로 답할 때 sqrt(x + sqrt(x + sqrt(x + ...))) = 1 에 대한 (연속성을 유지시켜주는) 답이 0보다는 1이 어울린다는 말입니다.
더 엄밀하고 깊게 말씀드리면 [sqrt(x + sqrt(x + sqrt(x + ...)))]라는 무한 표현을 사용한 것 자체가 수학적으로 모호한 표현(= 좋지 않은 표현 = 쓰면 안되는 표현)입니다.
그래서 sqrt(x + sqrt(x + sqrt(x + ...))) = 1의 대답이 관점에 따라 0이 될 수도 있고 1이 될 수도 있다는 것이죠.
아래 영상을 한 번 참고해보시지요. 무한 표현이 왜 좋지 않은 것인지에 대한 답을 알 수 있을 것입니다. :)
https://www.youtube.com/watch?v=mDPv7vGmWos
제가 위에서 답변을 잘못한 것이 있긴 하군요. ㅎㅎ
선생님 말씀대로 초항인 a_0를 0으로 셋팅하면 0이 되는게 맞습니다.
하지만 분문의 선생님의 질문은 초기 항을 셋팅한 것이 아니라 결과를 먼저 생각한 것이죠. [sqrt(x + sqrt(x + sqrt(x + ...))) = 1]
sqrt(x + sqrt(x + sqrt(x + ...))) = 1 식에서 어울리는 x가 무엇이냐에 대한 질문을 하신 겁니다.
점화식 [a_k = sqrt(0 + a_(k-1))] 에서 k를 무한대로 보내면 X = sqrt(0 + X)의 해가 무엇이냐의 질문이 되죠. 아시다시피 X는 0 또는 1 입니다.
본문의 sqrt(x + sqrt(x + sqrt(x + ...))) = 3 에서 x = 6 으로 답할 때 sqrt(x + sqrt(x + sqrt(x + ...))) = 1 에 대한 (연속성을 유지시켜주는) 답이 0보다는 1이 어울린다는 말입니다.
더 엄밀하고 깊게 말씀드리면 [sqrt(x + sqrt(x + sqrt(x + ...)))]라는 무한 표현을 사용한 것 자체가 수학적으로 모호한 표현(= 좋지 않은 표현 = 쓰면 안되는 표현)입니다.
그래서 sqrt(x + sqrt(x + sqrt(x + ...))) = 1의 대답이 관점에 따라 0이 될 수도 있고 1이 될 수도 있다는 것이죠.
아래 영상을 한 번 참고해보시지요. 무한 표현이 왜 좋지 않은 것인지에 대한 답을 알 수 있을 것입니다. :)
https://www.youtube.com/watch?v=mDPv7vGmWos
[지식in] 해석학적 역설들
| 목록 |
|