- 유머가 아닌 펌글, 영상 등 가볍게 볼 수 있는 글들도 게시가 가능합니다.
- 여러 회원들이 함께 사용하기 위해 각 회원당 하루 5개로 횟수제한이 있습니다.
- 특정인 비방성 자료는 삼가주십시오.
| Date | 22/01/26 03:03:13 |
| Name | Regenbogen |
| File #1 | 4E6B2B57_94AB_4DA0_83D8_ABB461B0FF7D.gif (7.6 KB), Download : 91 |
| File #2 | 2172F69B_02E5_4483_B5F8_CA15D9E7DBD5.jpeg (57.4 KB), Download : 53 |
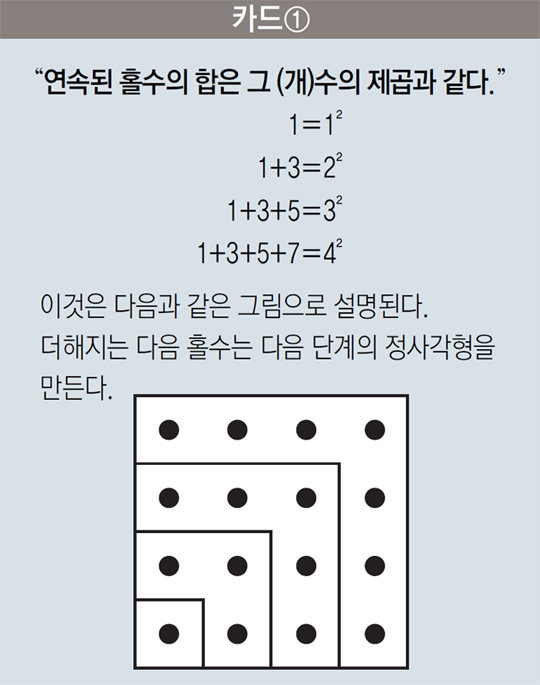
| Subject | 연속된 홀수의 합은 그 수의 제곱 |
|
처음 배웠을 때 되게 신기했고 증명하라고 할땐 출제자 때리고 싶었… 0
|
|
일반형: 1+3+...+(2n-1)=n²
좌변의 첫항과 마지막항을 더하고 하나씩 줄여 반복하면
1) n이 짝수: 좌변에는 2n이 n/2개 있으므로 2n*n/2=n²
2) n이 홀수: 좌변에는 2n이 (n-1)/2개 있고 n이 하나 더 있으므로 2n*{(n-1)/2}+n=n²-n+n=n². ㅁ
죄송합니다..
좌변의 첫항과 마지막항을 더하고 하나씩 줄여 반복하면
1) n이 짝수: 좌변에는 2n이 n/2개 있으므로 2n*n/2=n²
2) n이 홀수: 좌변에는 2n이 (n-1)/2개 있고 n이 하나 더 있으므로 2n*{(n-1)/2}+n=n²-n+n=n². ㅁ
죄송합니다..
N번째까지의 해당 규칙을 갖는 숫자의 합이 N^2임을 증명하려면
1 우선 1번째에서 1 = 1 = 1^2이므로 옳다
2 이제 N번째까지 옳다고 가정 즉 1 + 3 + ... (N개) = N^2
3 N+1번째에 더해지는 숫자는 2N + 1이고 N^2 + 2N + 1 = ( N + 1)^2이므로 N번째가 옳으면 N+1번째도 옳다
처음 시작할 때의 가정이 옳으므로 1번째가 옳으니 2번째도 옳고 2번째가 옳으니 3번째도 옳고... 무한반복
점화 완료 이로써 명제는 참이다 ㅁ
요런 증명(귀납법)도 있음둥...
1 우선 1번째에서 1 = 1 = 1^2이므로 옳다
2 이제 N번째까지 옳다고 가정 즉 1 + 3 + ... (N개) = N^2
3 N+1번째에 더해지는 숫자는 2N + 1이고 N^2 + 2N + 1 = ( N + 1)^2이므로 N번째가 옳으면 N+1번째도 옳다
처음 시작할 때의 가정이 옳으므로 1번째가 옳으니 2번째도 옳고 2번째가 옳으니 3번째도 옳고... 무한반복
점화 완료 이로써 명제는 참이다 ㅁ
요런 증명(귀납법)도 있음둥...
| 목록 |
|